[Read Paper] An efficient kernel transformation architecture for binary- and ternary-weight neural network inference
An efficient kernel transformation architecture for binary- and ternary-weight neural network inference
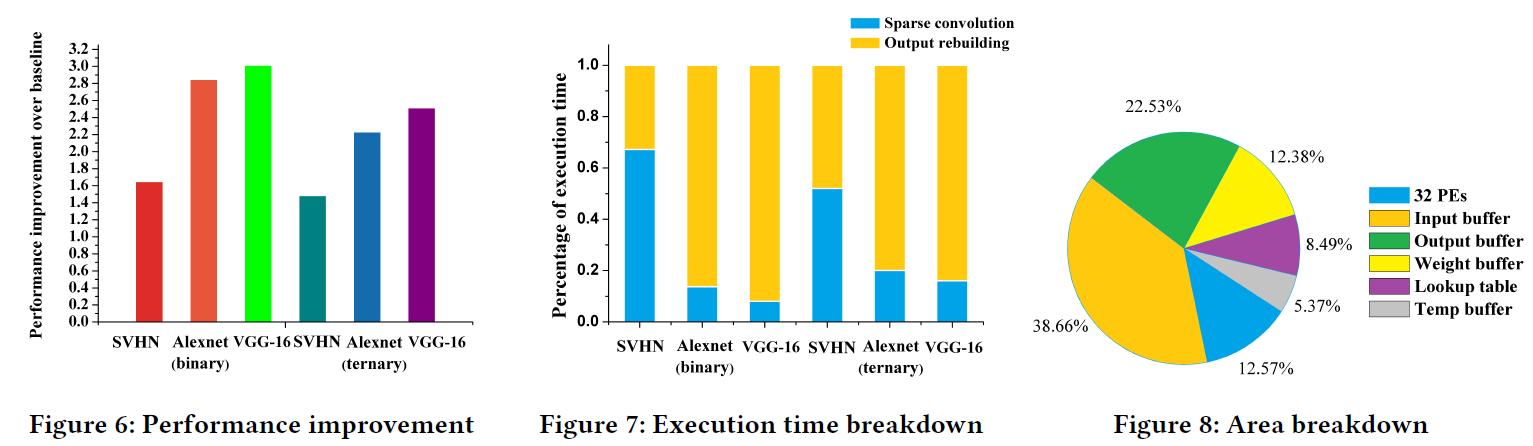
The initial kernels are transformed into much fewer and sparser ones, and the output feature maps are rebuilt from the immediate results. Overall, the number of total operations in convolution is reduced.
Background
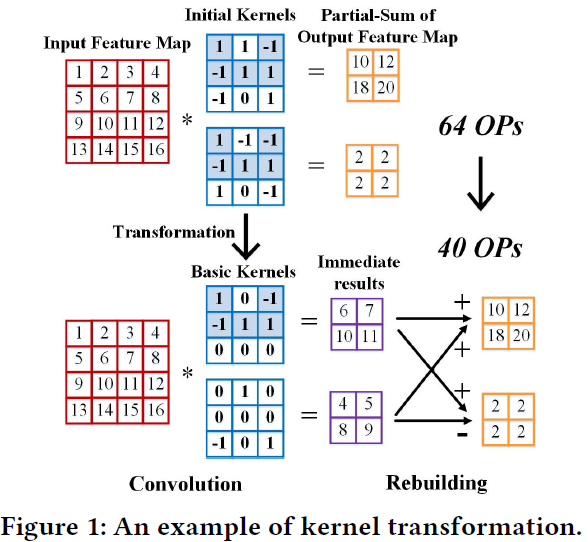
binary (1,-1) or ternary (1,0,-1)
Introduction
It is noteworthy that common fractions exist between these two kernels (shaded). By extracting them from initial kernels, two basic kernels with fewer non-zero weights are generated, and the final values are rebuilt from immediate results.
In this example, the number of kernels associated with one input feature map is only 2. As this number increases, more common fractions can be reused and higher reduction ratio can be obtained.
Problems
However, to efficiently implement this optimizing approach, several problems remain to be solved.
- Firstly, finding an optimal transformation is non-trivial. The number of kernels in modern CNNs ranges from tens to hundreds, which results in a large searching space. Efficient solving algorithms needs to be designed.
- Secondly, the basic kernels are highly sparse. The meaningless zeros should be excluded in the computation to save both time and energy.
- Thirdly, the rebuilding of final output feature maps occurs in an irregular pattern. Indices are needed to indicate the association between immediate results and output feature maps. Efficient scheduling on multiple processing elements (PEs) should also be designed to exploit data reuse.
Contributions
In this paper, we propose a kernel transformation architecture, making the following contributions:
- We introduce a novel approach to efficiently execute binary and ternary-weight CNN inference.
- Firstly, the input activations are convolved with fewer and sparser basic kernels.
- Then, these immediate results are selectively accumulated to rebuild final outputs feature maps.
- Benefited from elimination of most redundant operations, this approach improves both the performance and energy efficiency.
- We design a kernel transformation algorithm, which is an iterative searching based heuristic employed to extract common fractions in a set of ternary or binary kernels. With no change to the CNN inference formulas, it effectively reduces the total operation count, as well as the number of kernels.
- We design a specific hardware architecture to optimize the implementation of kernel-transformed binary- and ternary weight CNNs.
- We adopt an input stationary dataflow to improve data reuse and reduce memory access in convolution.
- Index-based weight compression is employed to process the sparse kernels.
- Efficient execution of irregular rebuilding is also enabled by this architecture.
A Kernel Transformation Architecture
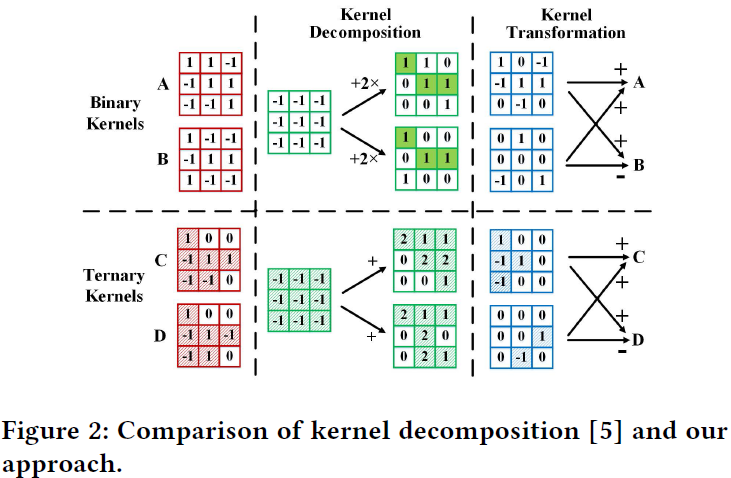
The execution flow of kernel transformation architecture is:
- (preprocessing) training CNNs into binary- or ternary-weight models →
- transforming initial kernels into fewer and sparser basic kernels →
- (runtime) computing immediate convolutional results of input activations and basic kernels →
- rebuilding output feature maps from immediate results.
Several Critical Problems
- Firstly, for each already trained network model, a near-optimal transformation solution should be found, which determines the upper-limit of inference speedup and energy-saving.
- Secondly, the transformed kernels are highly sparse,which should be exploited for better efficiency. Simply gating the clock can save unnecessary energy consumption brought by zero-valued weights, but the extra execution cycles cannot be reduced. Instead, index based weight compression can be employed to skip the accessing of zero-valued weights [4, 9], eliminating both the unnecessary time and energy consumption, and is adopted in this design.
- Thirdly, the association between basic and initial kernels is unpredictable, making the memory access pattern of output rebuilding irregular.
- During runtime, indices indicating proper immediate results must be provided to direct the rebuilding of output feature maps.
- Moreover, the scheduling of output channels on multiple processing elements (PEs) will also affect the performance of rebuilding.
Kernel Transformation Algorithm
Iterative pairwise matching algorithm [10] was proposed to solve the multiple constant multiplication (MCM) problem. Inspired by this algorithm, we develop an iterative searching based heuristic, which greedily extracting the common fraction that has the biggest overlap on all the kernels, until no more benefit can be obtained by elimination.

The input of the algorithm are the M set of N weights kernels of a specific convolutional layer, in which $M$ and $N$ represent the number of input channels and output channels, respectively. The output of the algorithm include the transformed sets of kernels associated with each input channel, with $N_i$ representing the number of transformed kernels in $i$th set. A $lookup table$ is also generated to record the transformation between initial kernels and transformed kernels. The algorithm operates on the $M$ set of kernels step-by-step.
Hardware Architecture
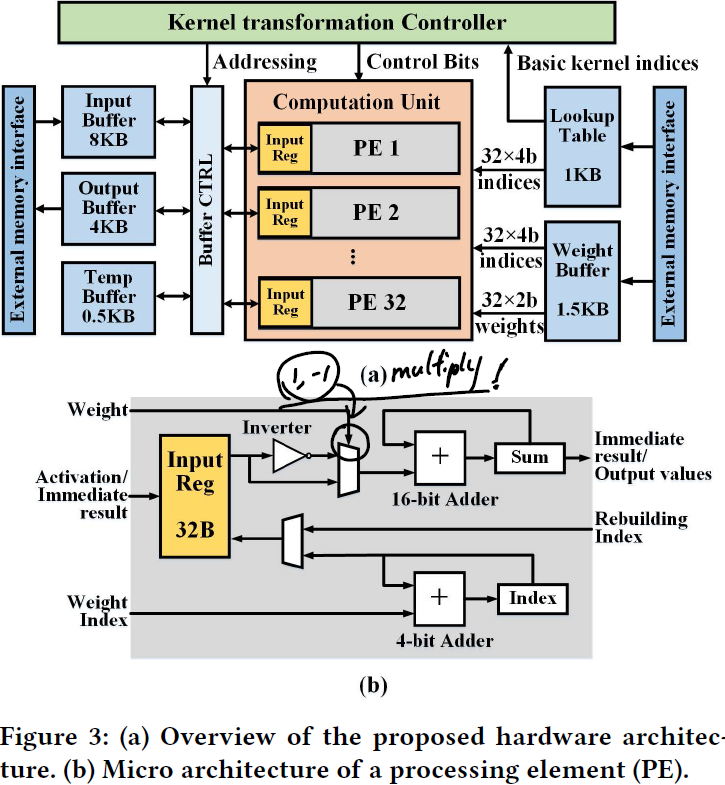
Each PE receives activations, sparse compressed weights and indices from respective buffers to execute convolution and rebuilding. The kernel transformation (overall) controller orchestrates the movement of data and the functioning of PEs. Compared with previous neural network accelerators, a temporary buffer is employed to store the convolutional results of basic kernels and a lookup table is employed for rebuilding final results.
Rebuilding of Output Feature Maps
The lookup table is used for the addressing of both temporary buffer and input register in each PE.
- It firstly provides a collection of indices of the immediate results (derived from basic kernels), which are required by the 32 output channels.
- Secondly, even with the immediate results imported to its input register, the PE cannot determine which values to accumulate, as the data requirement of rebuilding occurs in an irregular pattern. To solve this problem, for each PE, rebuilding indices are provided by the lookup table to directly control the access of its input register.
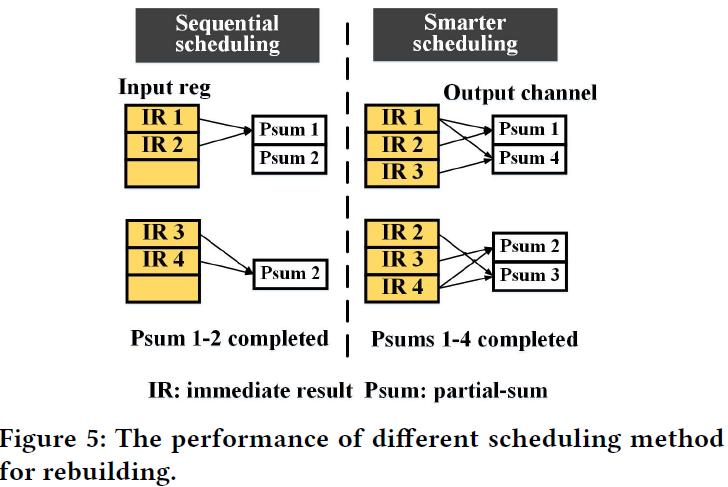
we rearrange the order of computation, based on their requirement on immediate results, in purpose of putting output channels that share more common input together as much as possible. As illustrated in Fig 5, for simplicity, assuming at most 3 values can be stored in input register, and two PEs are employed for rebuilding. If partial sum (Psum) 1 and 2 are grouped together, four immediate results (IRs) are required in total, and the input reg needs to be loaded for 2 times, idling the computation resource. Doubled throughput can be obtained by rearranging the scheduling order: 1 with 4, 2 with 3. In each group, the number of required IRs is 3, fitting the capacity of input buffer.
Results