[Read Paper] Systolic Arrays for VLSI
Systolic Arrays for VLSI
This paper is also published as Algorithms for VLSI Processor Arrays at introduction to VLSI systems. It proposes new multiprocessor structures and parallel algorithms for processing some basic matrix computations which are capable of pipelining matrix computations with optimal speed-up.
The pipelining aspect of the algorithms is most effective for band matrices with long bands.
By performance, this paper holds the view that time spent in I/O, control and data movement as well as arithmetic must all be considered.
The Basic Components and Array Structures
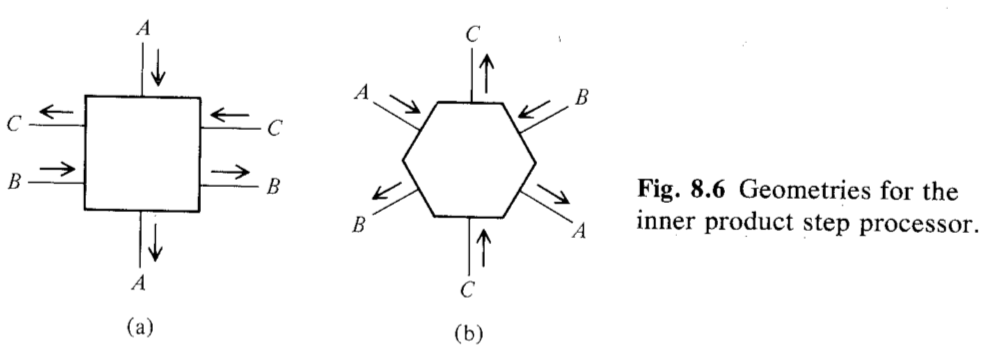
The Inner Product Step Processor
The single operation considered is inner product step $R_C ← R_C + R_A × R_B$. But we can implementation other kinds of "multiplication" or "add".
This processor should makes the input values for $R_A$, $R_B$, and $R_C$, respectively; computes the inner product $R_C ← R_C + R_A × R_B$; and makes the inputs values for $R_A$, $R_B$, together with the new value of $R_C$ available as outputs on the output lines.
Here are two types of the inner product step processor.
Processor Arrays
The basic network organization we shall adopt for processors is mesh-connected and all connections from a processor are to neighboring processors.
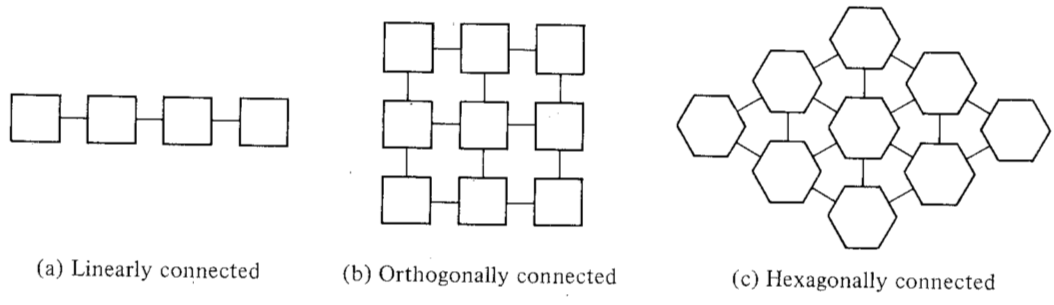
Processors lying on the boundary of the processor array may have external connections to the host memory.
Matrix-Vector Multiplication
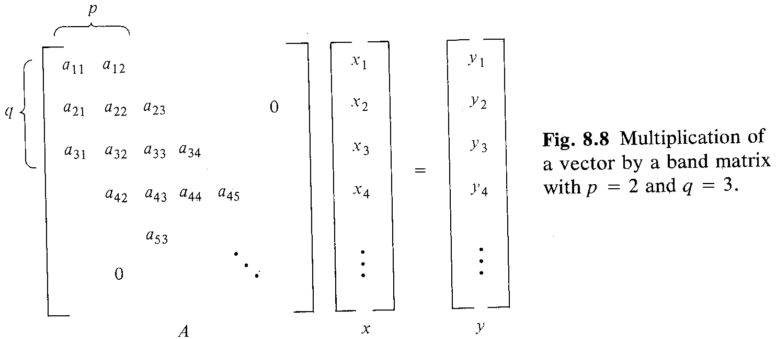
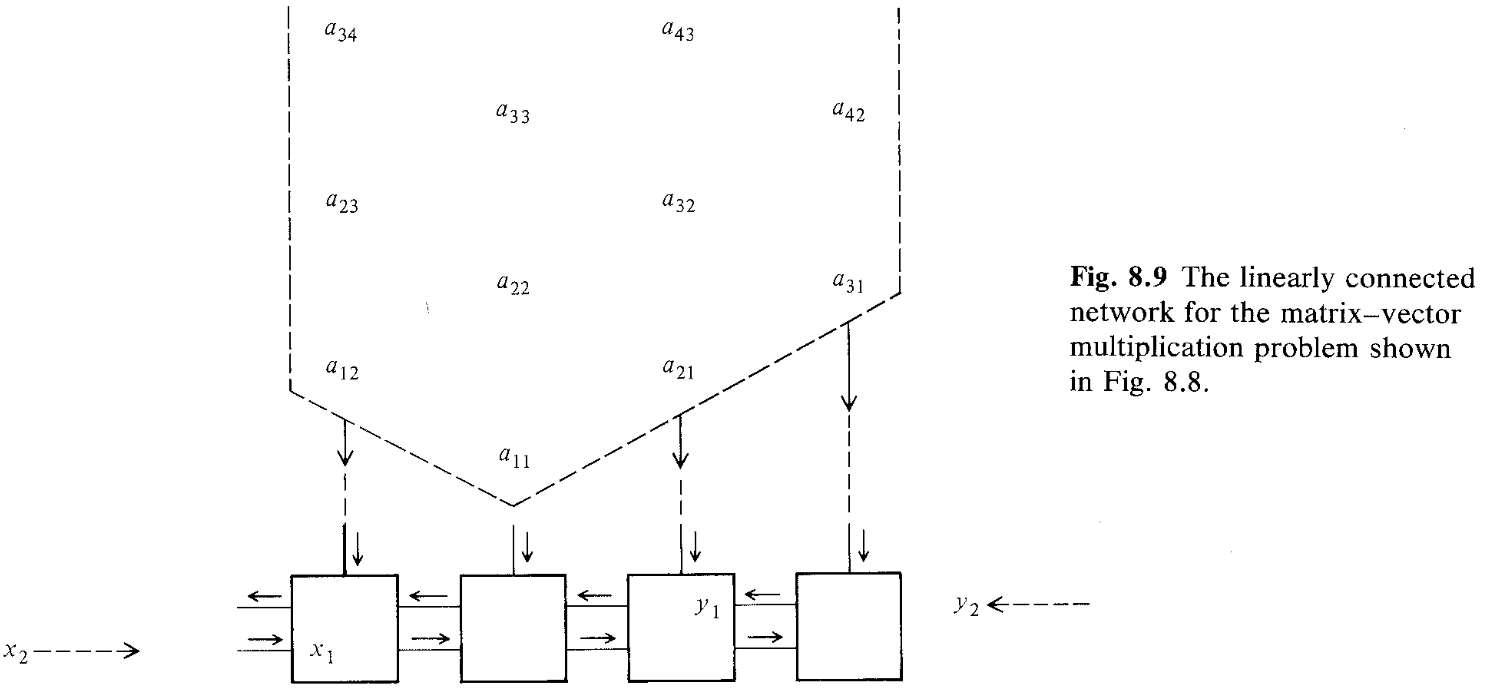
$w = p + q - 1$.
The utilization ratio is less than $50\%$ with $O(2n + w)$ time units, compared to $O(wn)$ time for the sequential algorithm on a uniprocessor.
Matrix Multiplication on a Hexagonal Array

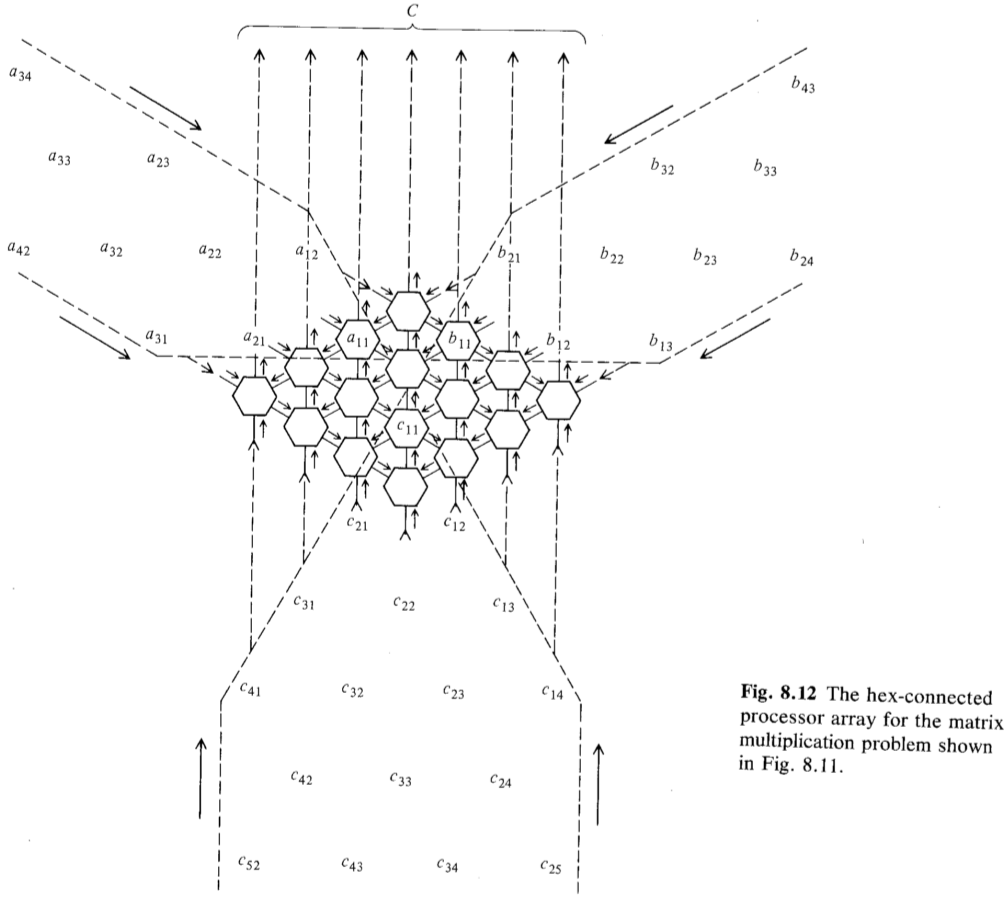
The utilization ratio is less than $1\over3$ with $O(3n + min(w_1, w_2))$ time units.
The LU-Decomposition of a Matrix on a Hexagonal Array
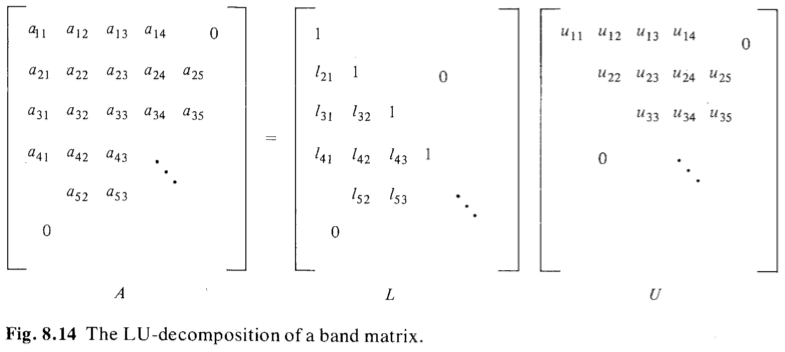
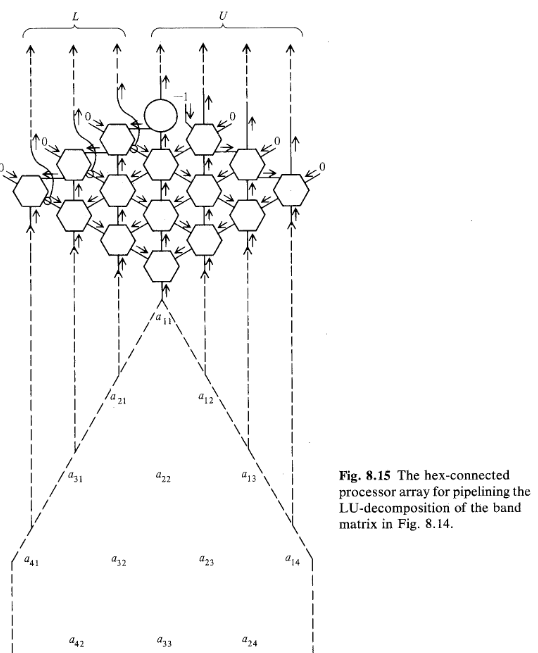
It can compute in $O(3n + min(p, q))$ time. If $A$ is an $n × n$ dense matrix, then the computation time is $4n$.
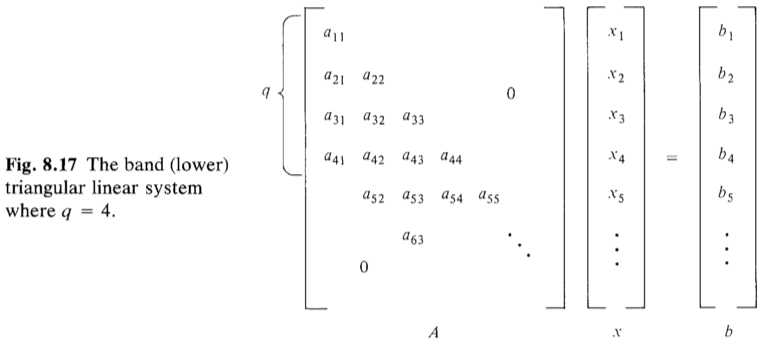
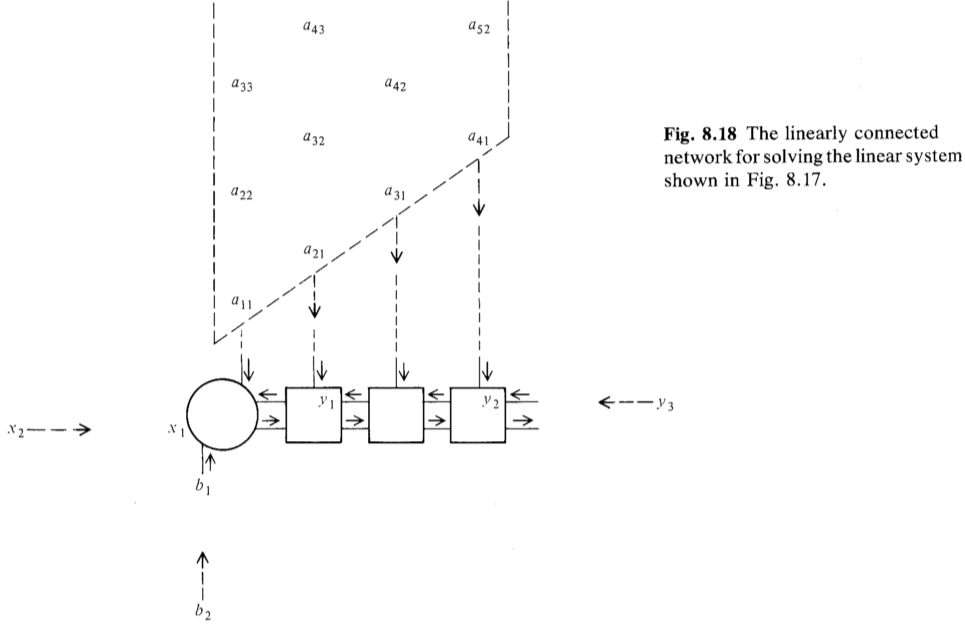
Triangular Linear Systems