[Read Paper] C-LSTM Enabling Efficient LSTM using Structured Compression Techniques on FPGAs
C-LSTM Enabling Efficient LSTM using Structured Compression Techniques on FPGAs
This paper introduce some methods to accelerate the LSTM targeted on FPGA.
It main utilize two methods:
- Block-Circulant Matrix
- smaller coarse-grained pipelines with double-buffers
Introduction
Previous Works
The previous work proposes to use a pruning based compression technique to reduce the model size and thus speedups the inference on FPGAs.
By creating ==dedicated pipelines, parallel processing units, customized bit width==, and etc., application designers can accelerate many workloads by orders of magnitude using FPGAs.
Problem
However, the random nature of the pruning technique transforms the dense matrices of the model to highly unstructured sparse ones, which leads to unbalanced computation and irregular memory accesses and thus hurts the overall performance and energy efficiency.
Solution
In contrast, we propose to use a structured compression technique which could not only reduce the LSTM model size but also eliminate the irregularities of computation and memory accesses.
- block-circulant to reduce the storage requirement from $O(k^2)$ to $O(k)$.
- Fast Fourier Transform reduces the computational complexity from $O(k2)$ to $O(klogk)$.
- an automatic optimization and synthesis framework called C-LSTM to port efficient LSTM designs onto FPGAs. The former one is in charge of iteratively training the compressed LSTM model and exploring the trade-offs between compression ratio and prediction accuracy.
Structured Compression
Block-Circulant Matrix
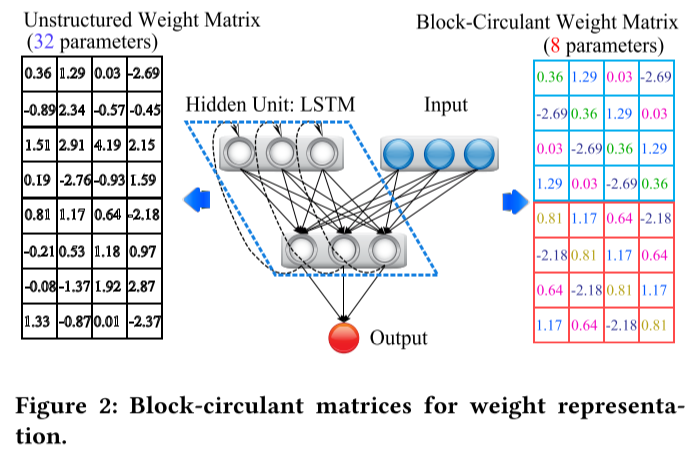
Figure 2 shows that the 8 × 4 weight matrix (on the left) is reformatted into a block-circulant matrix containing two 4 × 4 circulant matrices (on the right).
Each row vector of the circulant submatrix is a reformat of the first row vector.
larger block size leads to higher compression ratio and vice versa. However, high compression ratio may degrade the prediction accuracy.
FPGA Acceleration
Circulant Convolution Optimization
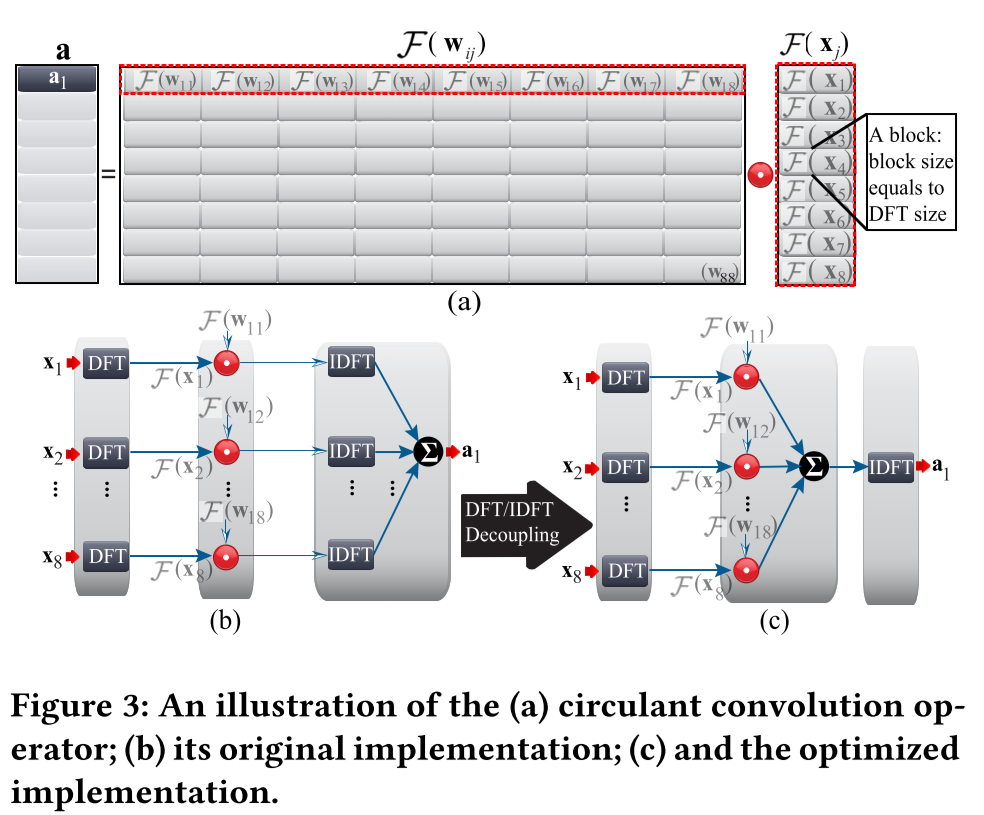
- Move IDFT operation outside the accumulation.
- pre-calculate the $F(w_{ij})$ values and store them in the BRAM buffers instead of computing them at runtime.
Operator Scheduling
Problem
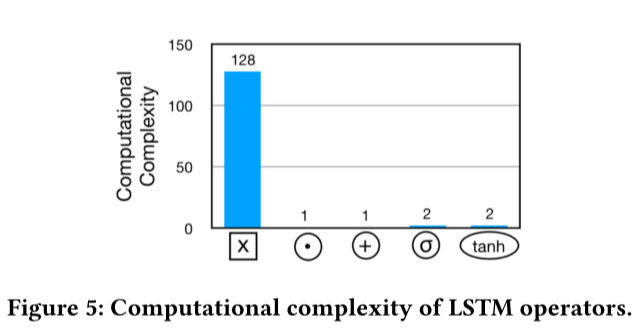
LSTMs exhibit a highly skewed distribution ofcomputation complexity among the primitive operators.
The computational complexity gap between the circulant convolution operator and element-wise multiply operator ⊙ is as large as 128 times. So, if we want to pipeline these two operators we must either boost the parallelism of the former operator or make the latter operator wait (idle) for the former one.
However, the reality is that the limited on-chip resources of FPGAs generally cannot sustain sufficient parallelism and the idle operators make the design inefficient.
Solution
==Breaking down the original single pipeline into several smaller coarse-grained pipelines and overlapping their execution time by inserting double-buffers foreach concatenated pipeline pair.==
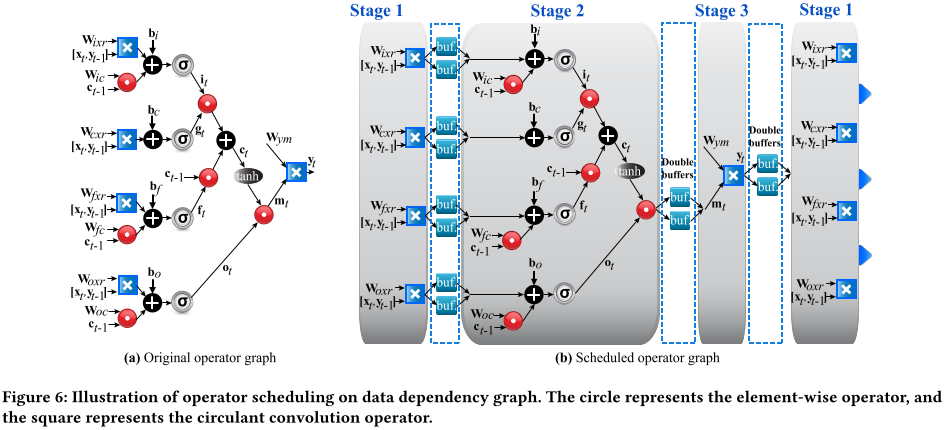
Since the overall throughput of this coarse-grained pipeline design is constrained by the slowest stage, we need to further determine the pipeline replication factor for each stage.
Further Reading
Liang Zhao, Siyu Liao, Yanzhi Wang, Jian Tang, and Bo Yuan. 2017. Theoretical Properties for Neural Networks with Weight Matrices of Low Displacement Rank. Arxiv preprint arxiv:1703.00144.