[Glean] Classifying Algorithms Based On Task Dependences

Published: December 14, 2020 by SingularityKChen (Last updated: December 14, 2020 )

• Categories:
• Glean 53

• Tags:
• Algorithms and parallel computing 2

• Classifying Algorithms Based On Task Dependences
  • Serial algorithms
  • Parallel algorithms
  • Serial–parallel algorithms (SPAs)
  • Nonserial–parallel algorithms (NSPAs)
  • Regular iterative algorithms (RIAs)

Classifying Algorithms Based On Task Dependences¹

Algorithms can be broadly classified based on task dependences:

1. Serial algorithms
2. Parallel algorithms
3. Serial–parallel algorithms (SPAs)
4. Nonserial–parallel algorithms (NSPAs)
5. Regular iterative algorithms (RIAs)

Serial algorithms

A serial algorithm is one where the tasks must be performed in series one after the other due to their data dependencies. The DG associated with such an algorithm looks like a long string or queue of dependent tasks.

Serial algorithms cannot be parallelized since the tasks must be executed sequentially. The only parallelization possible is when each task is broken down into parallelizable subtasks.

Parallel algorithms

A parallel algorithm is one where the tasks could all be performed in parallel at the same time due to their data independence. The DG associated with such an algorithm looks like a wide row of independent tasks.

Parallel algorithms are easily parallelized since all the tasks can be executed in parallel, provided there are enough computing resources.

Serial–parallel algorithms (SPAs)

An SPA is one where tasks are grouped in stages such that the tasks in each stage can be executed concurrently in parallel and the stages are executed sequentially.

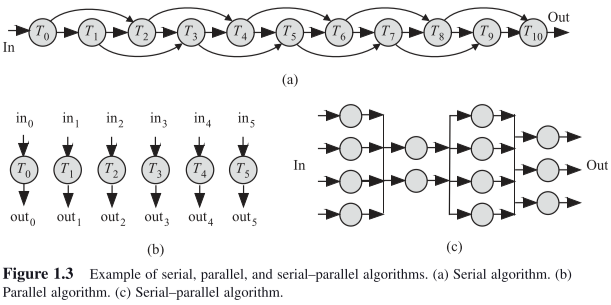
SPAs are parallelized by assigning each task in a stage to a software thread or hardware processing element. The stages themselves cannot be parallelized since they are serial in nature.

Nonserial–parallel algorithms (NSPAs)

Two types of graphs for NSPA:

1. DAG
2. Directed cyclic graph (DCG)

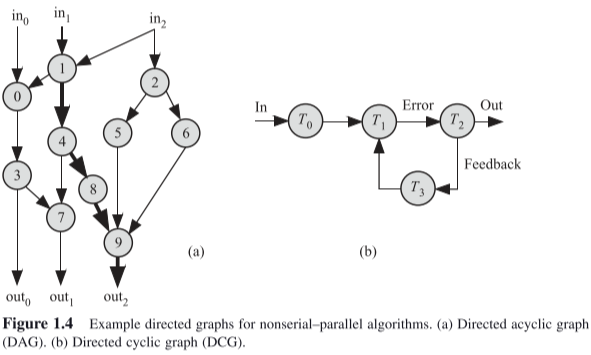
The DG of an algorithm gives us three important properties:

1. Work ( W ) , which describes the amount of processing work to be done to complete the algorithm
2. Depth ( D ) , which is also known as the critical path . Depth is defined as the maximum path length between any input node and any output node.
3. Parallelism ( P ) , which is also known as the degree of parallelism of the algorithm. Parallelism is defined as the maximum number of nodes that can be processed in parallel. The maximum number of parallel processors that could be active at any given time will not exceed B since anymore processors will not fi nd any tasks to execute.

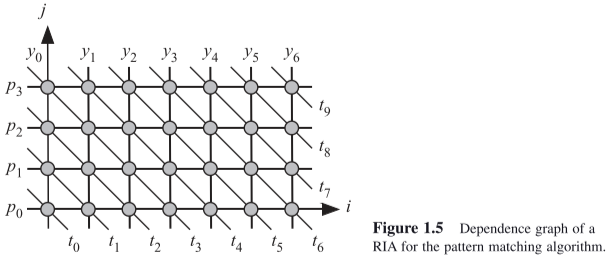
Regular iterative algorithms (RIAs)

Notice that for a RIA, we do not draw a DAG; instead, we use the dependence graph concept.

In a RIA, the dependencies among the tasks show a fi xed pattern. It is a trivial problem to parallelize a serial algorithm, a parallel algorithm, or even an SPA.

1. Gebali, Fayez. Algorithms and parallel computing. Vol. 84. John Wiley & Sons, 2011. ↩