[Glean] Algorithm DG (Directed Graph)
Published:
by
SingularityKChen
(Last updated:
)
- Categories:
- Glean 44
Algorithm DG (Directed Graph)1
Usually, an algorithm is graphically represented as a DG to illustrate the data dependencies among the algorithm tasks.
We use the DG to describe our algorithm in preference to the term “ dependence graph ” to highlight the fact that the algorithm variables flow as data between the tasks as indicated by the arrows of the DG.
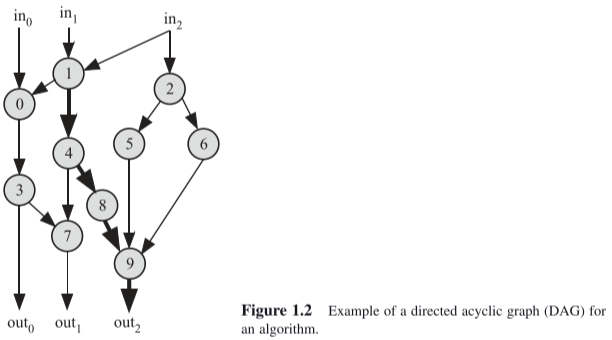
A DG is a set of nodes and directed edges. The nodes represent the tasks to be done by the algorithm, and the directed edges represent the data dependencies among the tasks. The start of an edge is the output of a task and the end of an edge the input to the task. An edge merely shows all the nodes that share a certain instance of the algorithm variable.
A directed acyclic graph (DAG) is a DG that has no cycles or loops.
An input edge in a DG is one that terminates on one or more nodes but does not start from any node. It represents one of the algorithm inputs. An output edge in a DG is one that starts from a node but does not terminate on any other node. It represents one of the algorithm outputs.
-
Gebali, Fayez. Algorithms and parallel computing. Vol. 84. John Wiley & Sons, 2011. ↩