[Read Paper] Attention Is All You Need
Published:
by
SingularityKChen
(Last updated:
)
- Categories:
- ReadPaper 30
- Tags:
- Attention 1
- NLP 1
- Transformer 1
- Attention Is All You Need
Attention Is All You Need12
Transformer: Encoder-Decoder Structure
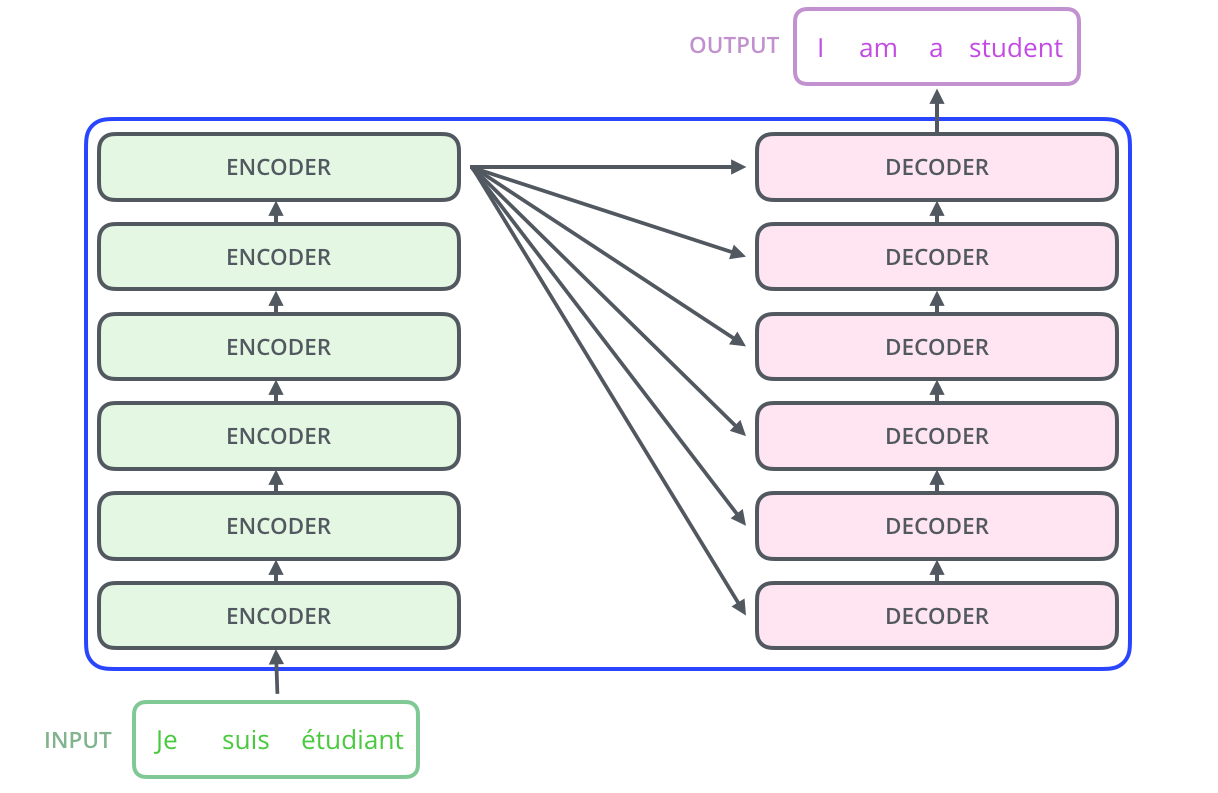The encoding component is a stack of encoders. The decoding component is a stack of decoders of the same number.
Structure of Encoder and Decoder
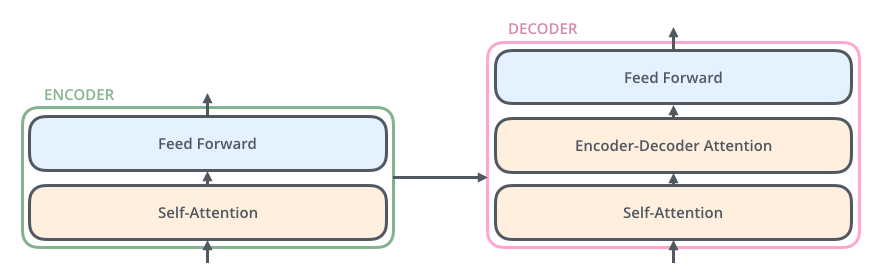
- Self-attention layer: a layer that helps the encoder look at other words in the input sentence as it encodes a specific word
- Encoder-decoder attention layer: helps the decoder focus on relevant parts of the input sentence
Sequential Coding: From Sentence to Vector
Every sentence is a matrix \(X = (x_1, x_2, ..., x_t)\) where \(x_i\) is the $i^{th}$ word vector.
We have three methods to encode these sequences.
RNN: LSTM, GRU, SRU
Doing this recursively: \(y_t=f(y_{t-1}, x_t)\)
Shortage:
- cannot computing parallelly
- can not study a global structure information as it's a Markov Decision Process.
CNN: Seq2Seq
Convolution: \(y_t = f(x_{t-1}, x_t, x_{t+1})\)
CNN is convenient to compute parallelly and can capture some local information, which can be increased with deeper layers.
Attention
\[y_t=f(x_t, A, B)\]Where $A$ and $B$ are other matrix. If \(A=B=X\), then it is called Self Attention, which means $y_t$ is computed by comparing $x_t$ with every words in the sentence.
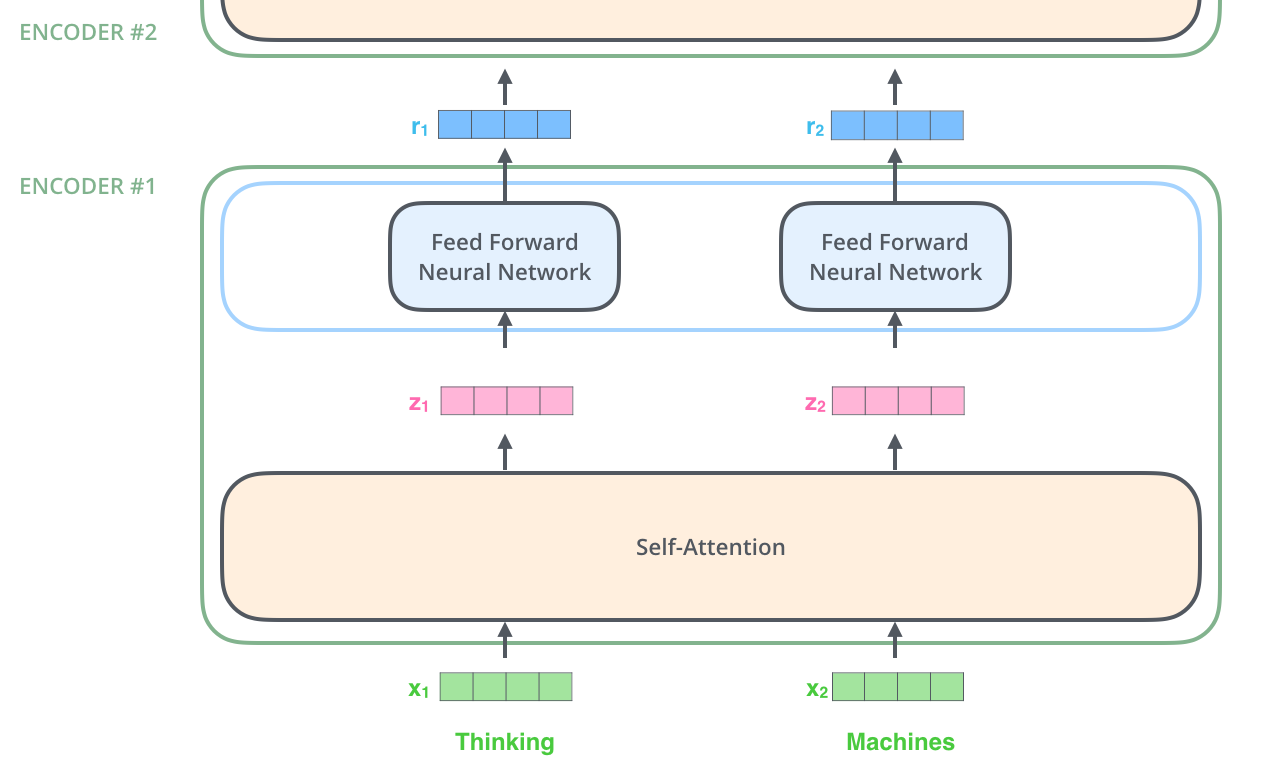
Encoding Component
An encoder receives a list of vectors as input. It processes this list by passing these vectors into a ‘self-attention’ layer, then into a feed-forward neural network, then sends out the output upwards to the next encoder.
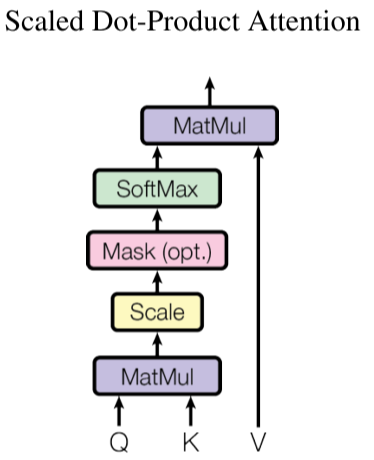
Computation of Attention
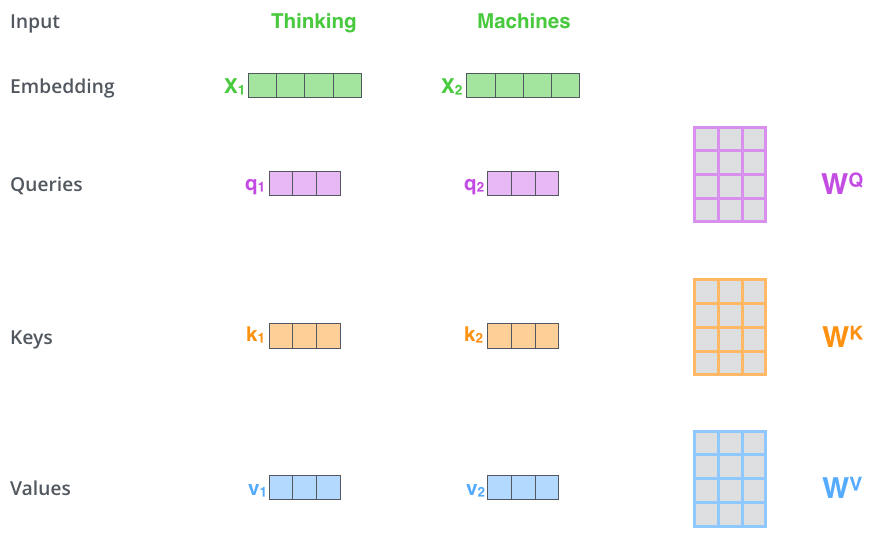
The first step in calculating self-attention is to create three vectors from each of the encoder’s input vectors.
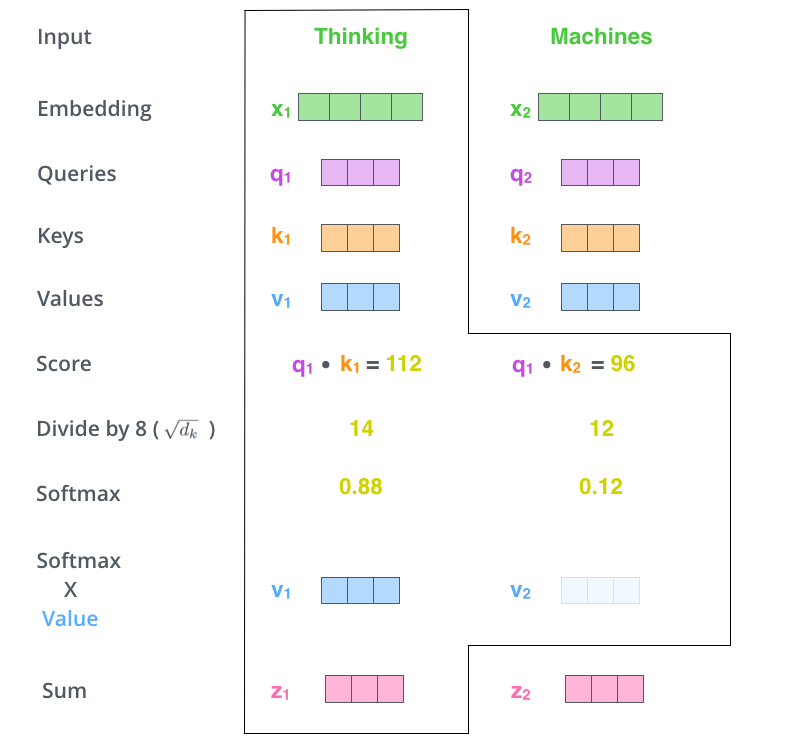
There are seven steps to compute the attention:
- translate words into embedding vectors
- compute three vectors $Q$, $K$, $V$, where $Q=X \times W^Q$, $K=X \times W^K$, $V=X \times W^V$.
- compute the dot product of $Q$ with $V$ of the respective word.
- normalize the scores by dividing the scores with $\sqrt{d_k}$.
- softmax normalizes the scores.
- multiply each value vector by the softmax score. The intuition here is to keep intact the values of the word(s) we want to focus on, and drown-out irrelevant words.
- sum up the weighted value vectors.
In fact, we can condense steps two through seven in one formula to calculate the outputs of the self-attention layer.
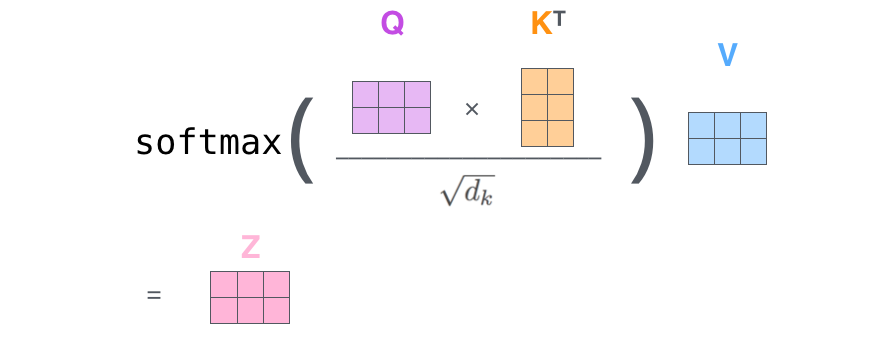
Actually, it is three matrix multiplication: $n \times d_k$, $d_k \times m$, $m \times d_v$, finally get a matrix $n \times d_v$. Therefore, attention layer is a process that encode $n \times d_k$ sequence $Q$ into a new $n \times d_v$ sequence.
Multi-Head Attention
The paper further refined the self-attention layer by adding a mechanism called “multi-headed” attention. This improves the performance of the attention layer in two ways:
- It expands the model’s ability to focus on different positions.
- It gives the attention layer multiple “representation subspaces”.
Shortages of Attention Layers
Though attention is able to capture the global information by comparing the sequences while the computation complex is \(O(n^2)\), however, it still has some shortages:
- both multi-head attention and residual structure are from CNN
- can not model the location information.
- in some situation, applications relies on partial information.
Therefore, maybe we can combine attention with CNN or RNN and fully utilize their own advantages.
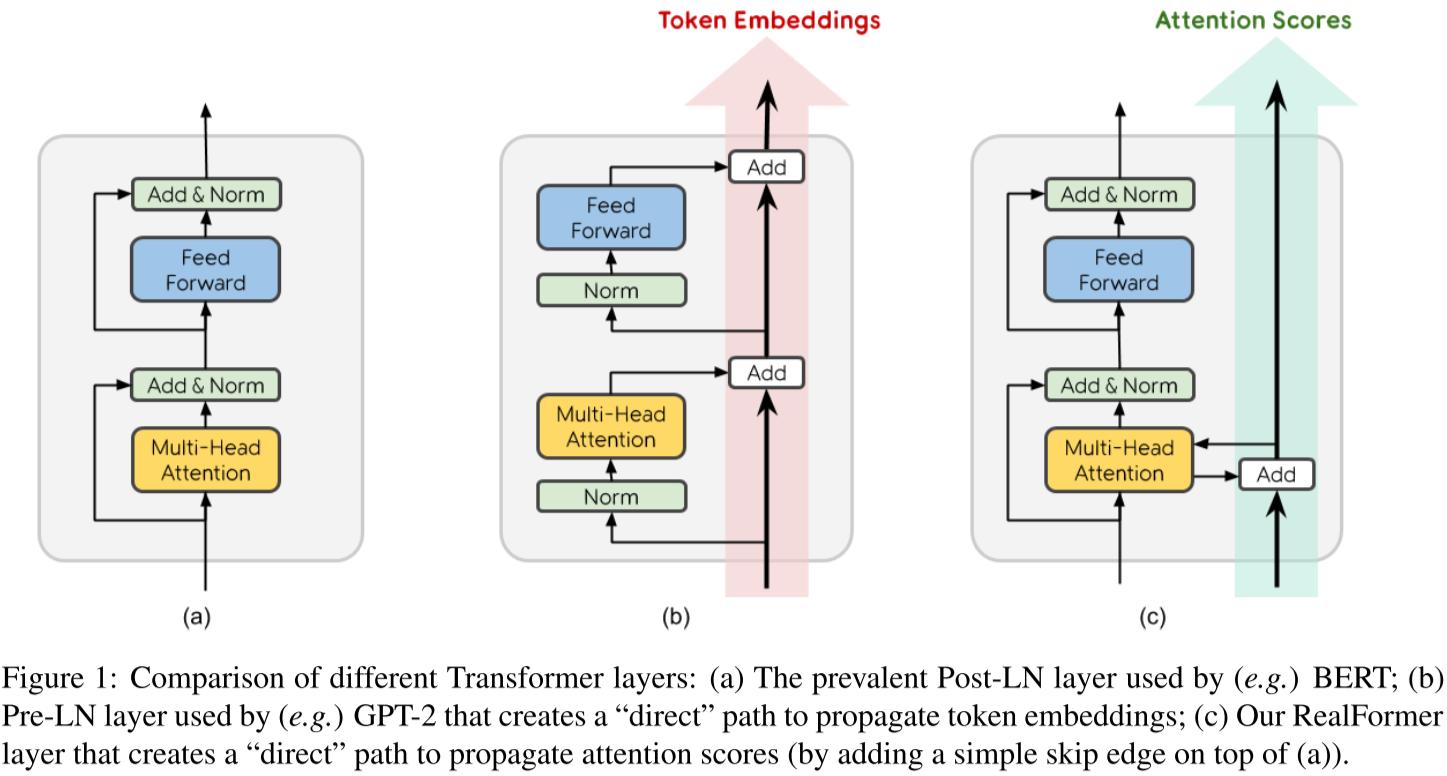
One Improvement: RealFormer: Transformer Likes Residual Attention
Attention:
\[Attention(Q_n, K_n, V_n)=softmax(A_n)V_n, A_n=\frac{Q_nK_n^T}{\sqrt{d_k}}\]New attention:
\[Attention(Q_n, K_n, V_n)=softmax(A_n)V_n, A_n=\frac{Q_nK_n^T}{\sqrt{d_k}}+A_{n-1}\]