[Glean] Posit: A Potential Replacement for IEEE 754

Published: by Creative Commons Licence (Last updated: )

Posit: A Potential Replacement for IEEE 7541

Introduction

In February 2017, Gustafson officially introduced Unum type III, posits and valids. Similar size posits when compared to floats offer a bigger dynamic range and more fraction bits for accuracy. Posits have variable-sized index and mantissa bitfields, with the split being specified by a "regime" indicator.2

Four parts

Posits consist of four parts: sign, regime, exponent, and fraction (a.k.a. significand/mantissa). For a $n$-bit posit, regime can be of length 2 to $(n − 1)$. The format of the regime is such that it is a repetition of a same-sign bit and terminated by a different-sign bit. 2

The sign bit is 0 for positive numbers and 1 for negative ones. The number of regime bits is dynamic following a special encoding. After the sign bit, the regime includes a run of 0 or 1, which is terminated by an opposite bit ($r̄$) or at the end of the number format. Similarly, the number of bits for the exponent and fraction is dynamic. A posit number includes the exponent and fraction only if necessary.1

General posit format for finite, nonzero values-color codes.

Let $m$ be the number of identical bits in the regime bits (amber color). If the first bit is zero, the number of zeros ($m$) represents a negative value ($-m$). Otherwise, the number of ones minus one ($m-1$) represents a positive value $(m-1)$. The regime bits realize a scale factor of useedk, where $useed = 2^{2^{es}}$.1

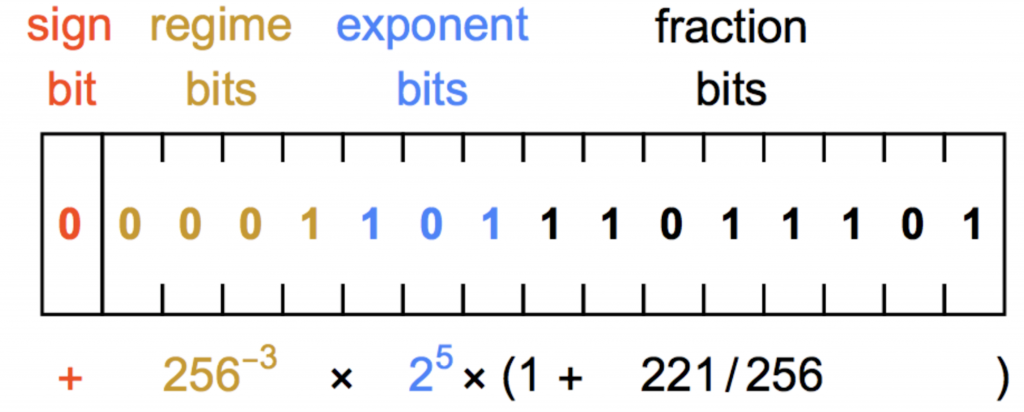
One example

As for the exponents bits, I think it's predefined.

The recommended posit sizes and corresponding exponent bits and quire sizes:2

Posit size (bits) Number of exponent bits Quire size (bits)
8 0 32
16 1 128
32 2 512
64 3 2048

Note: 32-bit posit is expected to be sufficient to solve almost all classes of applications.

  1. P. Behnam, M. N. B. on Apr 21, and 2020, “Posit: A Potential Replacement for IEEE 754,” SIGARCH, Apr. 21, 2020. https://www.sigarch.org/posit-a-potential-replacement-for-ieee-754/ (accessed Jan. 18, 2021). ↩ ↩2 ↩3

  2. “Unum (number format),” Wikipedia. Dec. 29, 2020, Accessed: Jan. 18, 2021. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Unum_(number_format)&oldid=996875965. ↩ ↩2 ↩3