[Survey] GEMM, Strassen and Winograd Fast Convolution Algorithms

Published: by Creative Commons Licence (Last updated: )

GEMM, Strassen and Winograd Fast Convolution Algorithms

GEMM and Img2Col

DaVinci1 accelerated convolution by translating conv2d into GEMM by Img2Col.

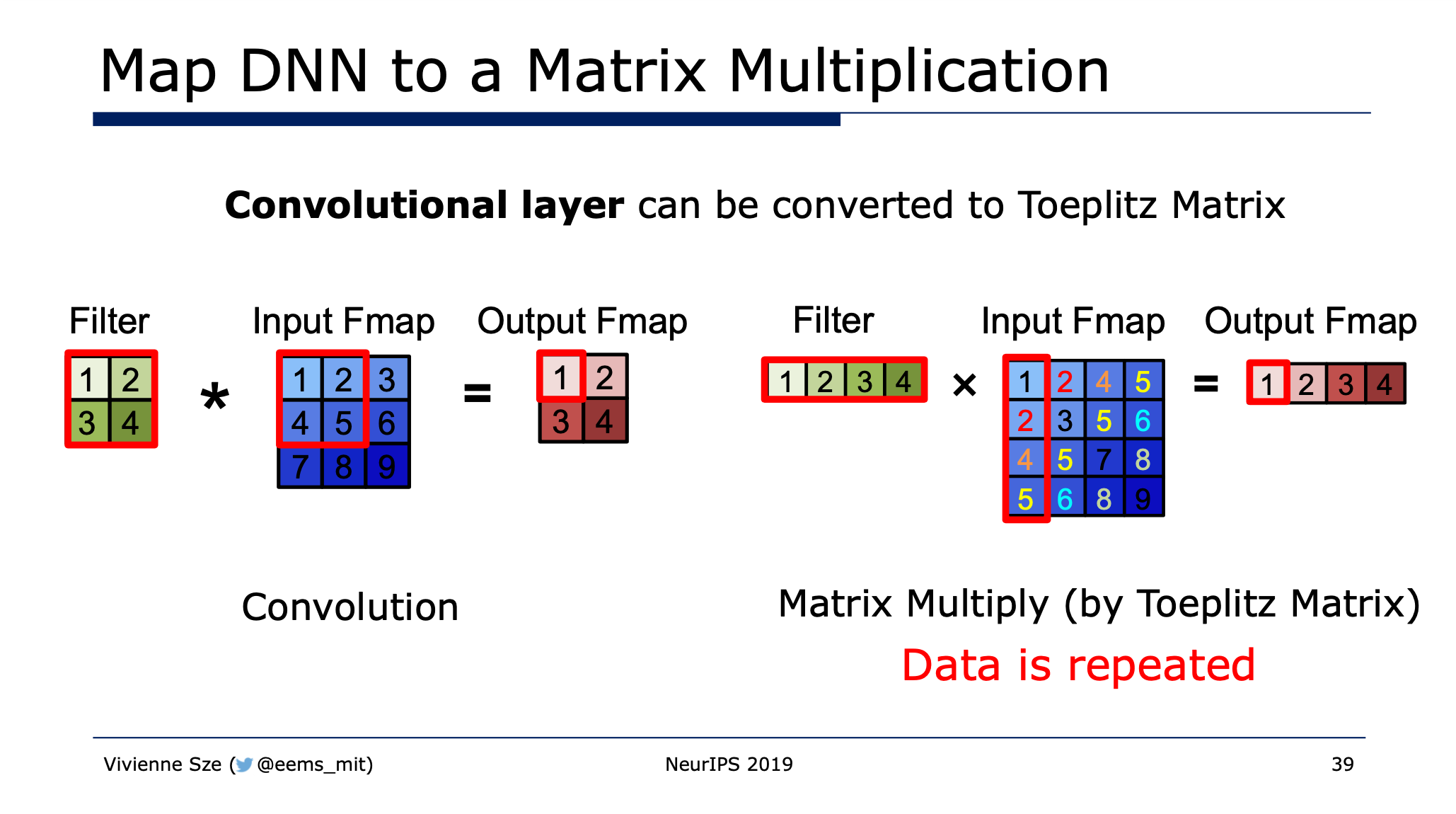
Img2Col

Strassen Algorithm

Cong and Xiao2 introduce Strassen algorithm to recursively compute 2x2 Matrix Mult using only 7 multiplications.

Computation Optimization

Boyer3 also provides another version of Strassen matrix multiplication algorithm.

Strassen-Winograd's matrix multiplication algorithm

Task Dependency Graph

Winograd Algorithm

3x3 Stride 1 Conv

Lavin4 first used Winograd’ s minimal filtering algorithms for convolutional neural networks.

F(2x2,3x3)

From equation 7 we can found that we can simply implement those transforming via shift and add.

The number of additions and constant multiplications required by the minimal Winograd transforms increases quadratically with the tile size. Thus for large tiles, the complexity of the transforms will overwhelm any savings in the number of multiplications.

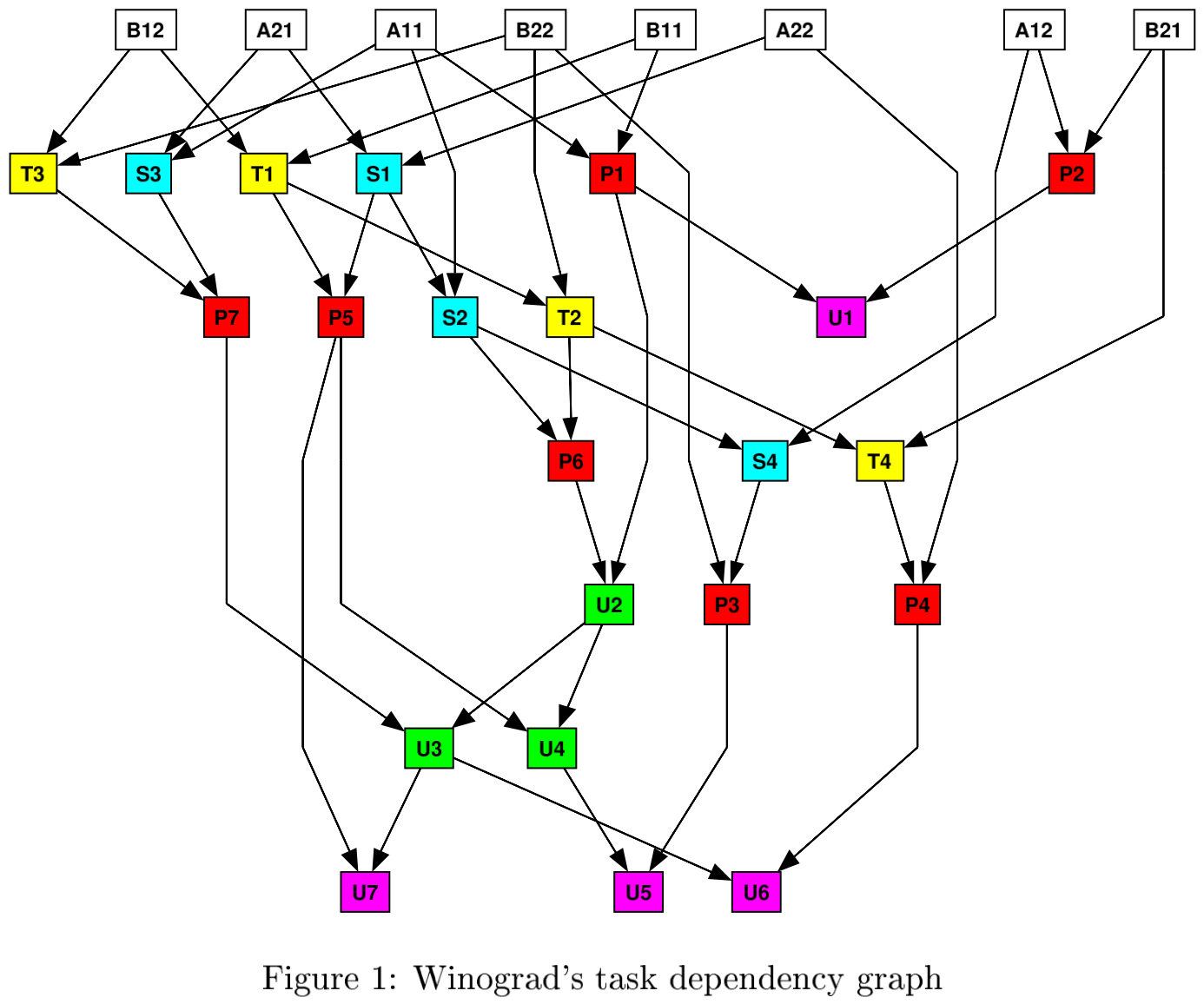
Kala5 proposed a Winograd-GEMM architecture that both able to compute Winograd accelerated Convolution and full connection layers that are computed using general element-wise matrix multiplication (GEMM).

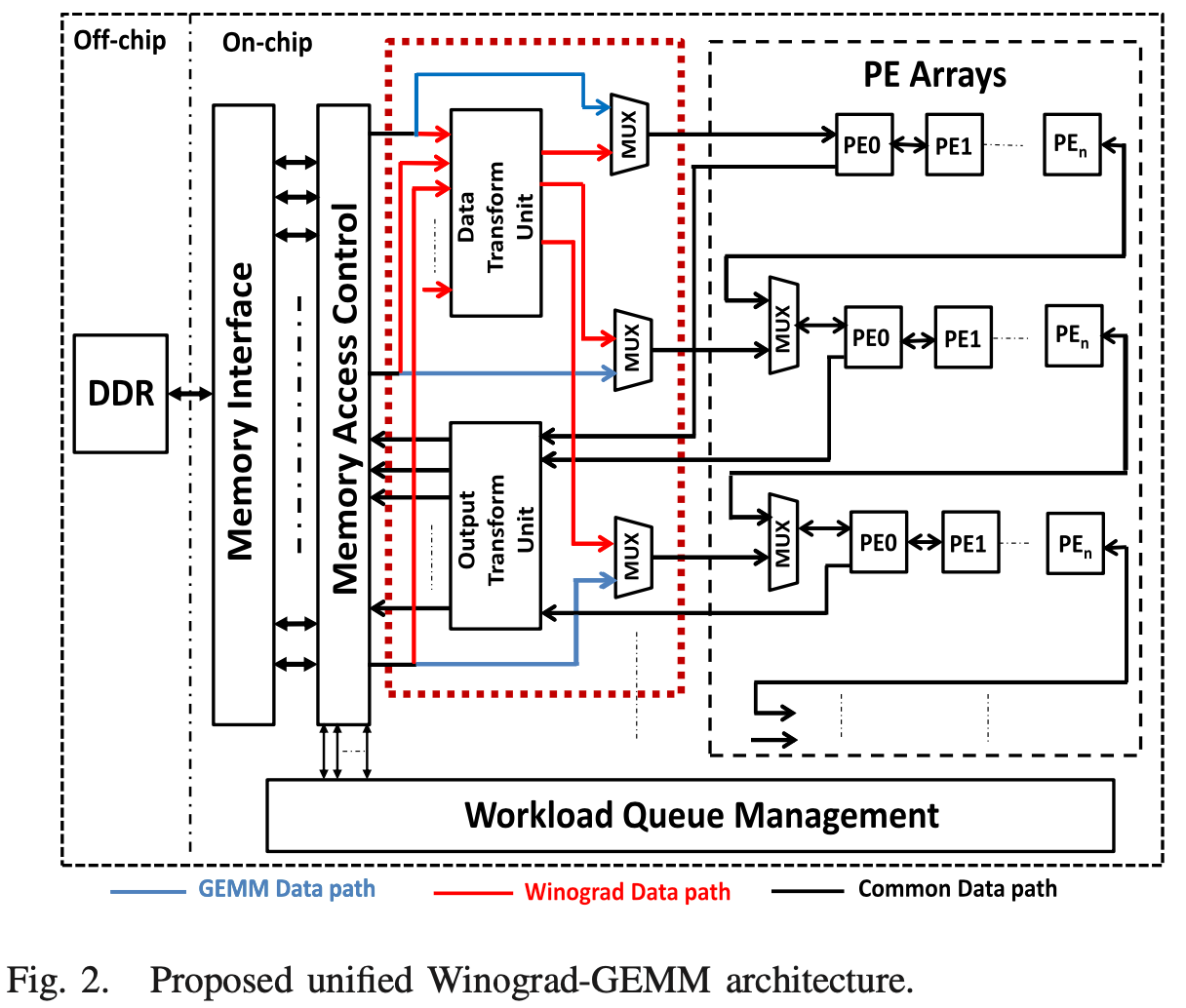
Winograd-GEMM architecture

Ahmad and Pasha 6 tried to explore both feature overlap and kernel reuse.

Method stub for fast-conv using P CEs, exploiting both feature overlap and kernel reuse

Lu7 wrote a section to introduce the design space exploration of Winograd hardware.

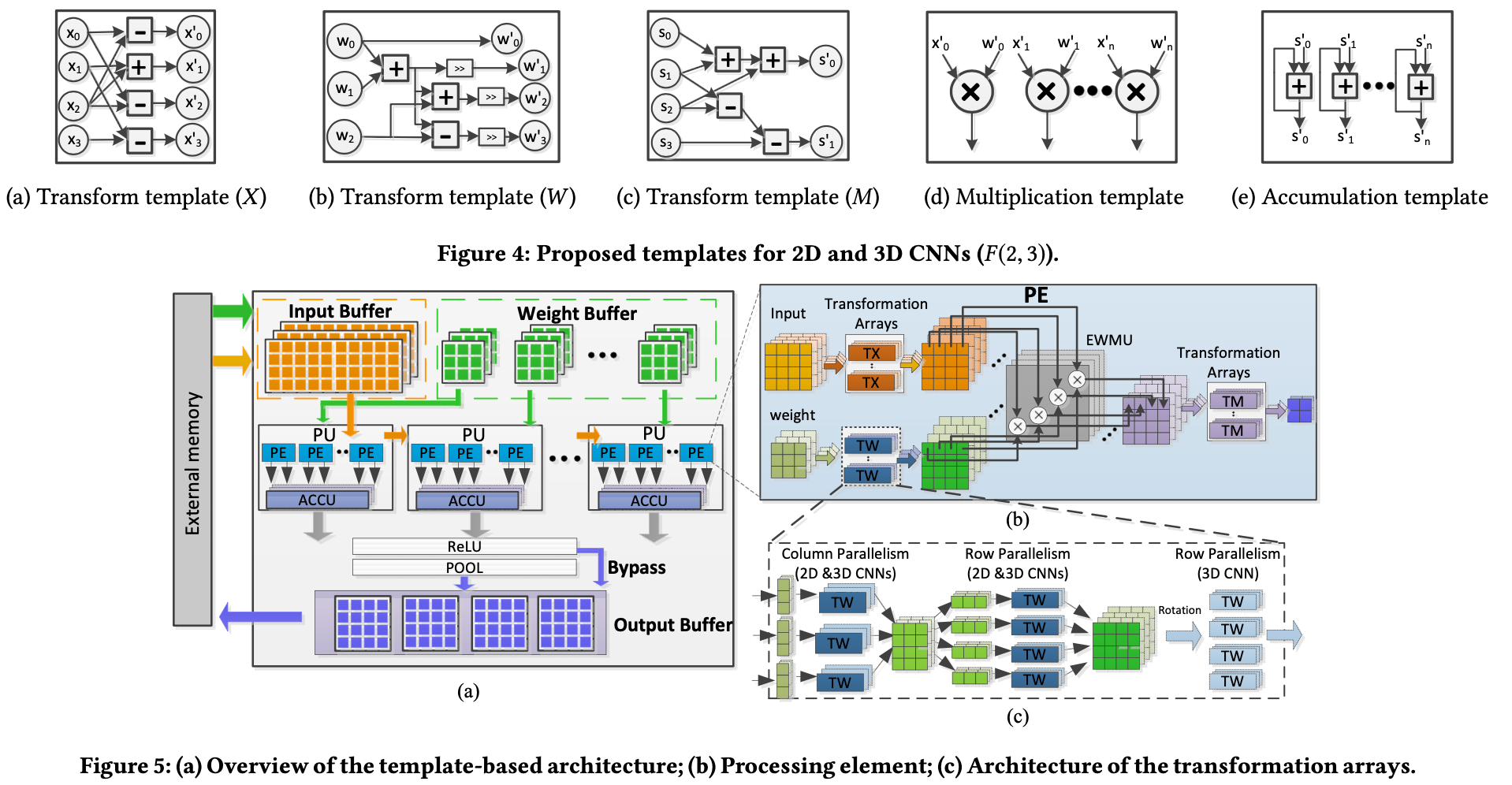
Shen8 demonstrated a template-based architecture for F(2,3) Winograd operation.

7x7, 3x3 Stride 2 Conv

There are several stride of 2 convolution layers in the neural networks as well.

Yepez9 proposed transform kernels of size 3, 5 and 7 with stride of 2 for 1D, 2D and 3D convolution. Compared to regular convolutions, the implementations for stride 2 are 1.44 times faster for a 3 × 3 kernel, 2.04× faster for a 5 × 5 kernel, 2.42× faster for a 7 × 7 kernel, and 1.73× faster for a 3 × 3 × 3 kernel.

1D

In 1-D convolution with stride 2, odd positions of the input are multiplied with odd positions of the kernel, and even-position input elements are multiplied with even-position kernel elements; no multiplication between odd-position and even-position elements occurs. Thus, we can separate the input and kernel elements into two groups: odd and even. Using these groupings, it is possible to convert a convolution of stride 2 into two convolutions of stride 1.

Size 3 Kernel: F(2,2) Winograd and normal mult

Size 5 Kernel: F(2,3) and F(2,2) Winograd

Size 7 Kernel: F(2,4) and F(2,3) Winograd

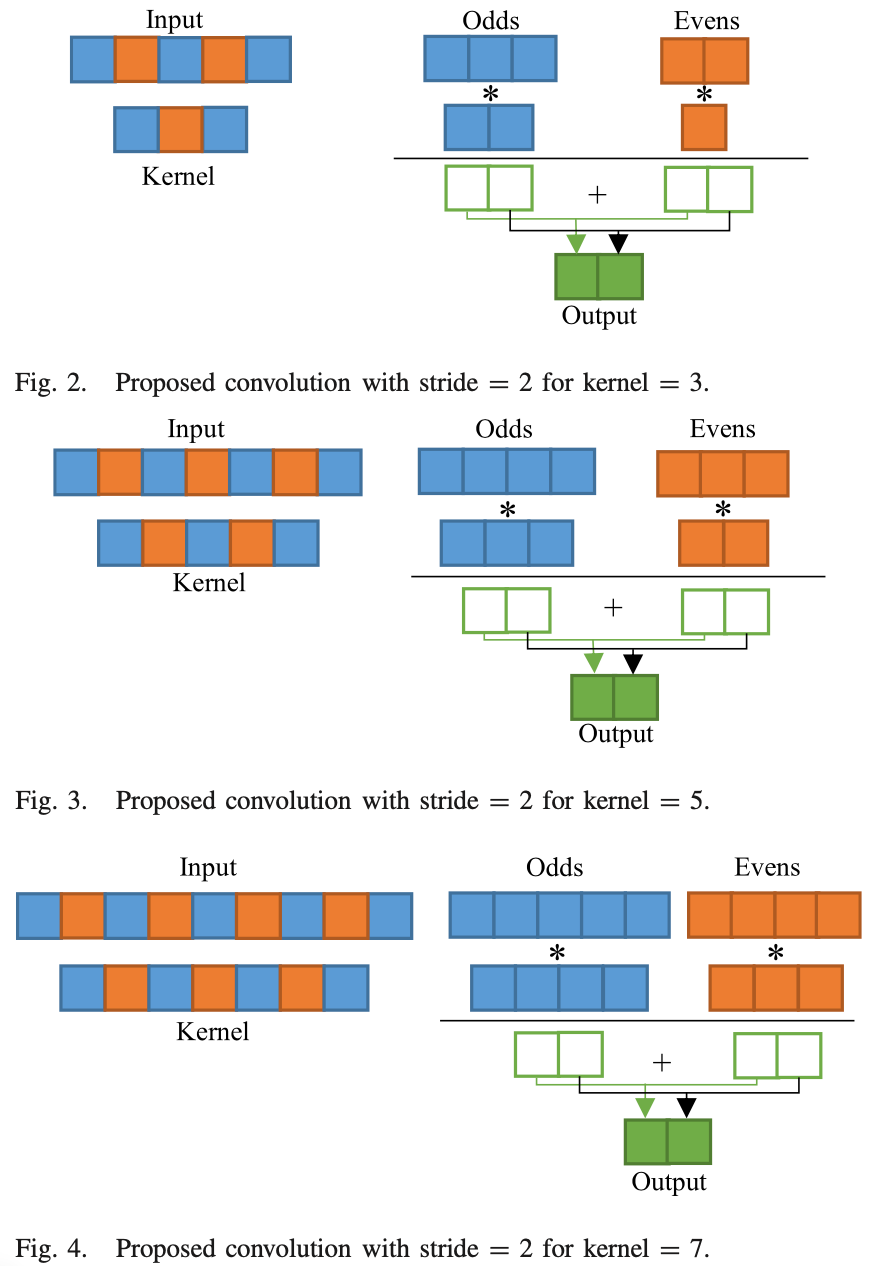
1D stride 2

2D

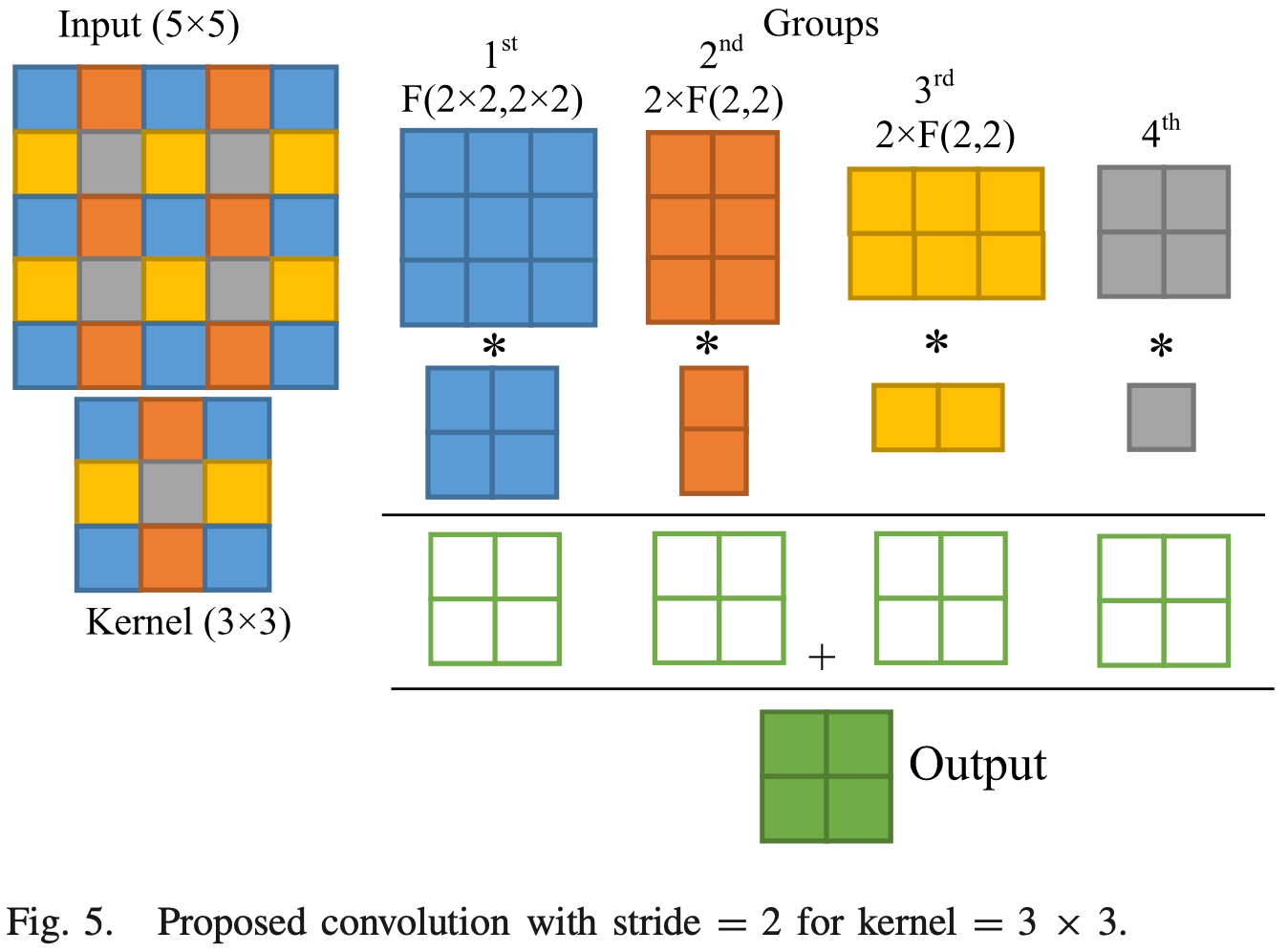
stride = 2 for kernel = 3 × 3

#####

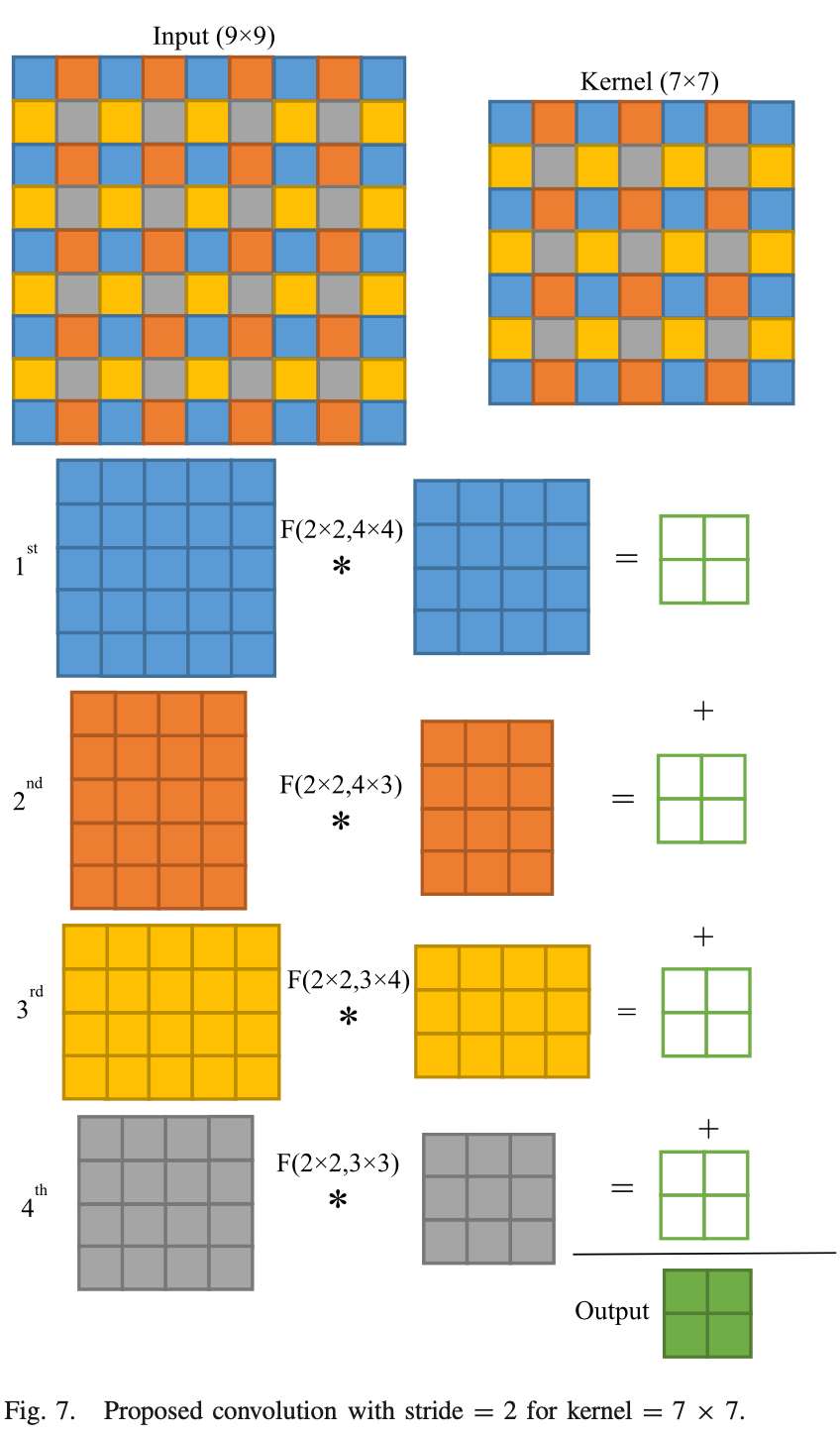
stride = 2 for kernel = 7 × 7

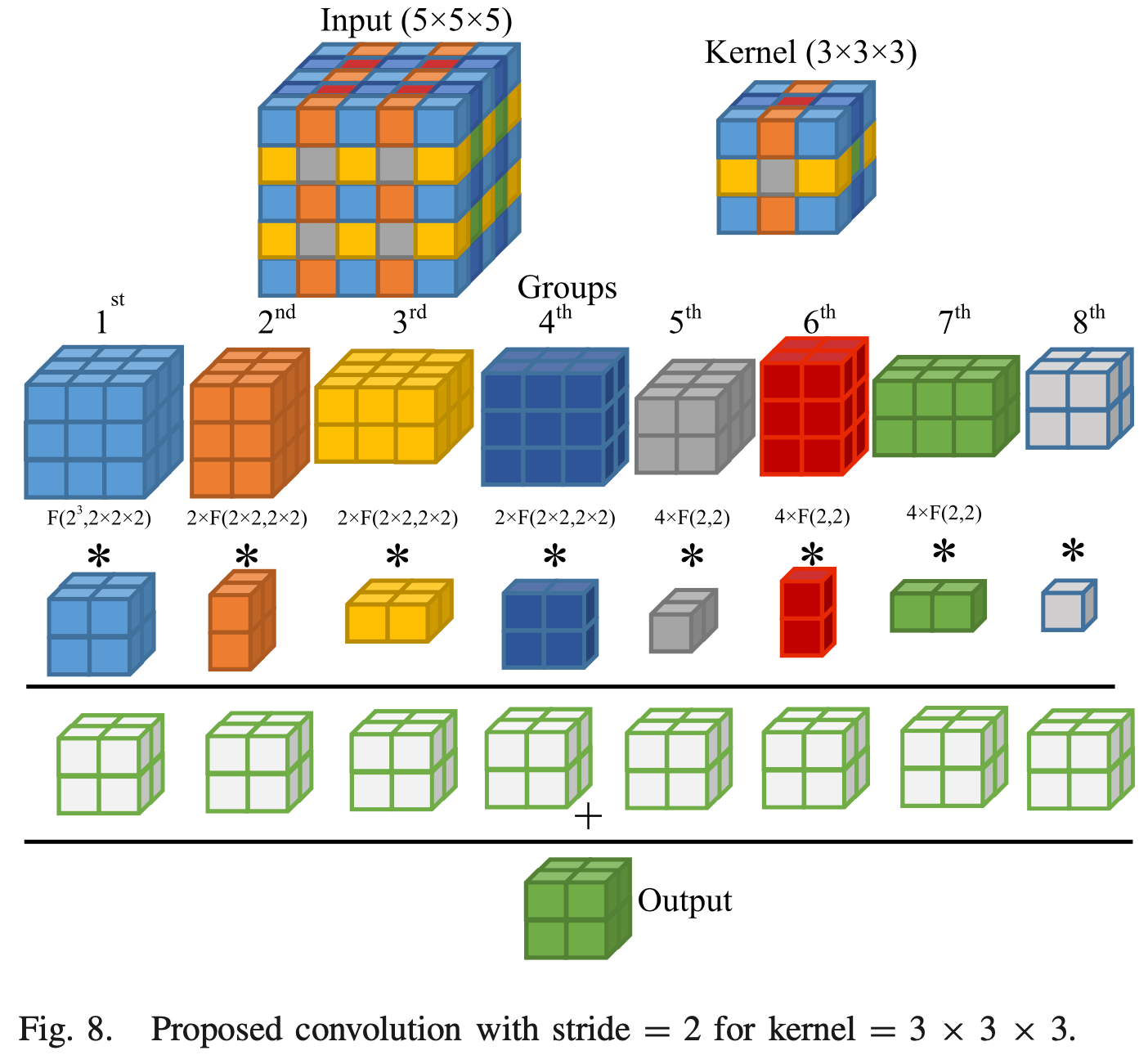
3D Conv

Deng10 and Yepez9 proposed Winograd algorithm that fit 3D convolution.

3D Winograd Algorithm

stride = 2 for kernel = 3 × 3 × 3

Explore Sparsity

Liu11 and Shi12 also explored the sparsity of Winograd MM operations.

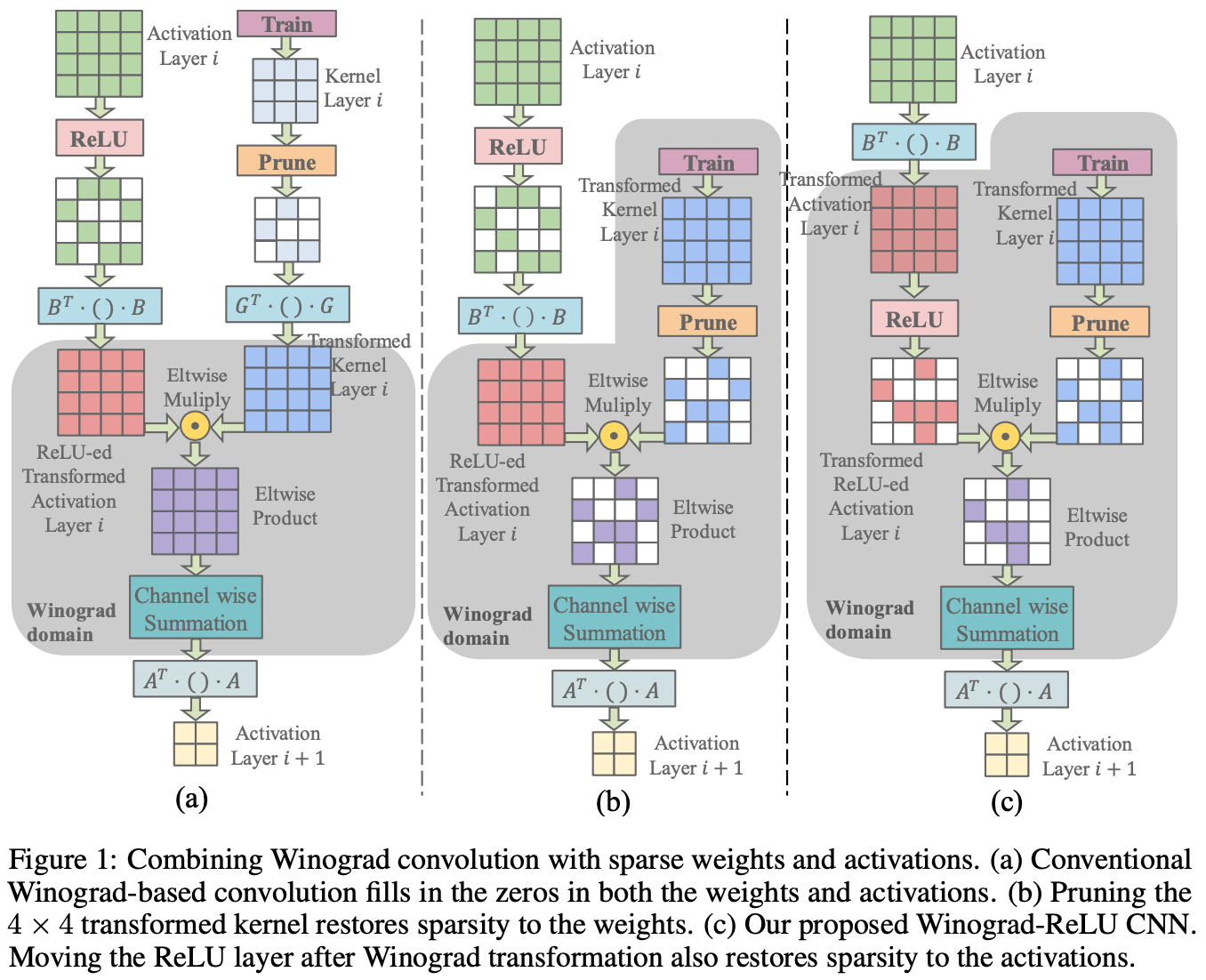
Combining Winograd convolution with sparse weights and activations.

Strassen–Winograd Algorithm

Zhao13 combined the Strassen and Winograd algorithms together.

Algorithm 1 shows the Strassen Algorithm. Here the block matrix multiplications is still the normal convolution or GEMM. Then in algorithm 2, the Convolution is replaced by Winograd operation.

Implementation of the Strassen Algorithm

Implementation of the Strassen–Winograd Algorithm

Reference

  1. H. Liao, J. Tu, J. Xia, and X. Zhou, “DaVinci: A Scalable Architecture for Neural Network Computing,” in 2019 IEEE Hot Chips 31 Symposium (HCS), Aug. 2019, pp. 1–44. ↩

  2. J. Cong and B. Xiao, “Minimizing Computation in Convolutional Neural Networks,” in Artificial Neural Networks and Machine Learning – ICANN 2014, vol. 8681, S. Wermter, C. Weber, W. Duch, T. Honkela, P. Koprinkova-Hristova, S. Magg, G. Palm, and A. E. P. Villa, Eds. Cham: Springer International Publishing, 2014, pp. 281–290. ↩

  3. B. Boyer, J.-G. Dumas, C. Pernet, and W. Zhou, “Memory efficient scheduling of Strassen-Winograd’s matrix multiplication algorithm,” arXiv:0707.2347 [cs], May 2009. ↩

  4. A. Lavin and S. Gray, “Fast Algorithms for Convolutional Neural Networks,” arXiv:1509.09308 [cs], Nov. 2015. ↩

  5. S. Kala, B. R. Jose, J. Mathew, and S. Nalesh, “High-Performance CNN Accelerator on FPGA Using Unified Winograd-GEMM Architecture,” IEEE Trans. VLSI Syst., vol. 27, no. 12, pp. 2816–2828, Dec. 2019. ↩

  6. A. Ahmad and M. A. Pasha, “FFConv: An FPGA-based Accelerator for Fast Convolution Layers in Convolutional Neural Networks,” ACM Trans. Embed. Comput. Syst., vol. 19, no. 2, pp. 1–24, Mar. 2020. ↩

  7. L. Lu, Y. Liang, Q. Xiao, and S. Yan, “Evaluating Fast Algorithms for Convolutional Neural Networks on FPGAs,” in 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, Apr. 2017, pp. 101–108. ↩

  8. J. Shen, Y. Huang, Z. Wang, Y. Qiao, M. Wen, and C. Zhang, “Towards a Uniform Template-based Architecture for Accelerating 2D and 3D CNNs on FPGA,” in Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey CALIFORNIA USA, Feb. 2018, pp. 97–106. ↩

  9. J. Yepez and S.-B. Ko, “Stride 2 1-D, 2-D, and 3-D Winograd for Convolutional Neural Networks,” IEEE Trans. VLSI Syst., vol. 28, no. 4, pp. 853–863, Apr. 2020. ↩ ↩2

  10. H. Deng, J. Wang, H. Ye, S. Xiao, X. Meng, and Z. Yu, “3D-VNPU: A Flexible Accelerator for 2D/3D CNNs on FPGA,” in 2021 IEEE 29th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Orlando, FL, USA, May 2021, pp. 181–185. ↩

  11. X. Liu, J. Pool, S. Han, and W. J. Dally, “Efficient Sparse-Winograd Convolutional Neural Networks,” arXiv:1802.06367 [cs], Feb. 2018. ↩

  12. F. Shi, H. Li, Y. Gao, B. Kuschner, and S.-C. Zhu, “Sparse Winograd Convolutional Neural Networks on Small-scale Systolic Arrays,” in Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside CA USA, Feb. 2019, pp. 118–118. ↩

  13. Y. Zhao, D. Wang, and L. Wang, “Convolution Accelerator Designs Using Fast Algorithms,” Algorithms, vol. 12, no. 5, p. 112, May 2019. ↩