[Read Paper] BitFlow: Exploiting Vector Parallelism for Binary Neural Networks on CPU

Published: by Creative Commons Licence (Last updated: )

BitFlow: Exploiting Vector Parallelism for Binary Neural Networks on CPU

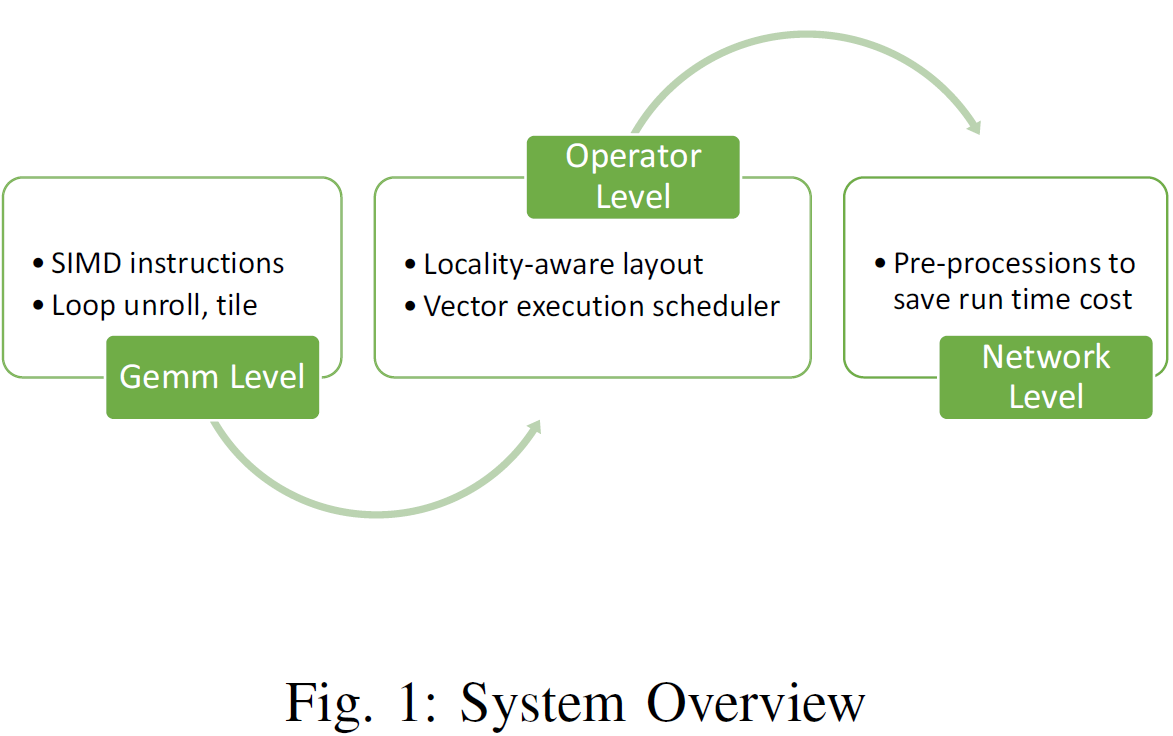
BitFlow System Overview

  • Gemm-Level Optimization: fuse binarization, bit-packing, and transposition into a single operation
  • Operator-Level Optimization: BitFlow abandons the conventional image-to-column method due to low arithmetic intensity and unfriendly pattern for bitwise operations when applied to binary convolution, and introduces a new class of algorithm named Pressed-Conv using locality-aware layout and vector parallelism for efficient binary convolution. It uses SIMD efficiently with a general vector execution scheduler.
  • Network-Level Optimization: compared with full precision DNN, BNN introduces binarization and bit-packing stages.
    • conduct binarization and bit-packing of weights during network initialization
    • pre-allocate all the memory needed for storing the output
    • intermediate results by analysis of the neural network as a static computational graph

Neural Network Compression and Acceleration Methods and Background of BNNs

Network Compression and Acceleration

  • Network Pruning: remove non-informative neural connections. the parameters below a certain threshold are removed to form a sparse network, and then the network is re-trained for the remaining connections.
  • Network Quantization
  • Binary Neural Networks: Computationally intensive Floating-point Multiply and Add operations (FMAs) are replaced by XOR (for multiplications) and bit-count (for accumulations), enabling significant computational speedup.

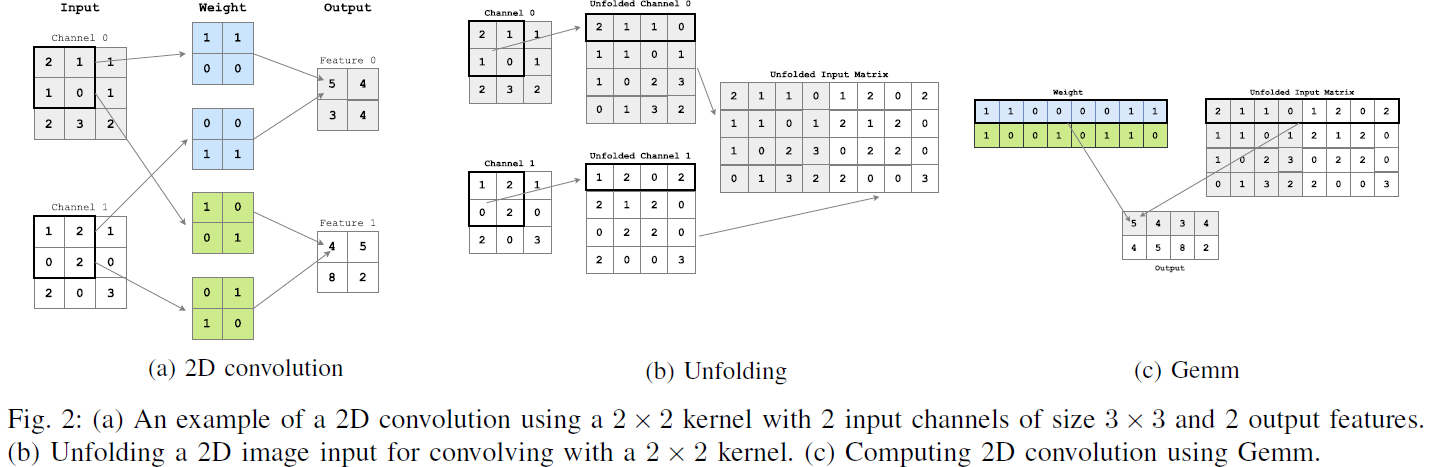
Convolution Operation

  • Unfold
  • Gemm

Efficient binary neural network operators

Weights and activations are {−1, +1}, but at the hardware level they must be encoded as {0, 1}.

Limits of Image-to-column for Binary Convolution

  • Overhead brought by the unfolding procedure, which reduces the maximum achievable fraction of the intrinsic Arithmetic Intensity (AIT) of the convolution operation. Arithmetic Intensity (AIT) refers to the ratio of the number of arithmetic operations to the number of memory operations in a computation. The unfolding procedure increases the size of the input while the unfolded input need to be stored before the Gemm, doubling the number of memory accesses to the unfolded input
  • after the input tensor is unfolded into a matrix of $M ×N$, $N$ won’t be multiple of 32 in most cases, making bit-packing and SIMD execution inefficient.

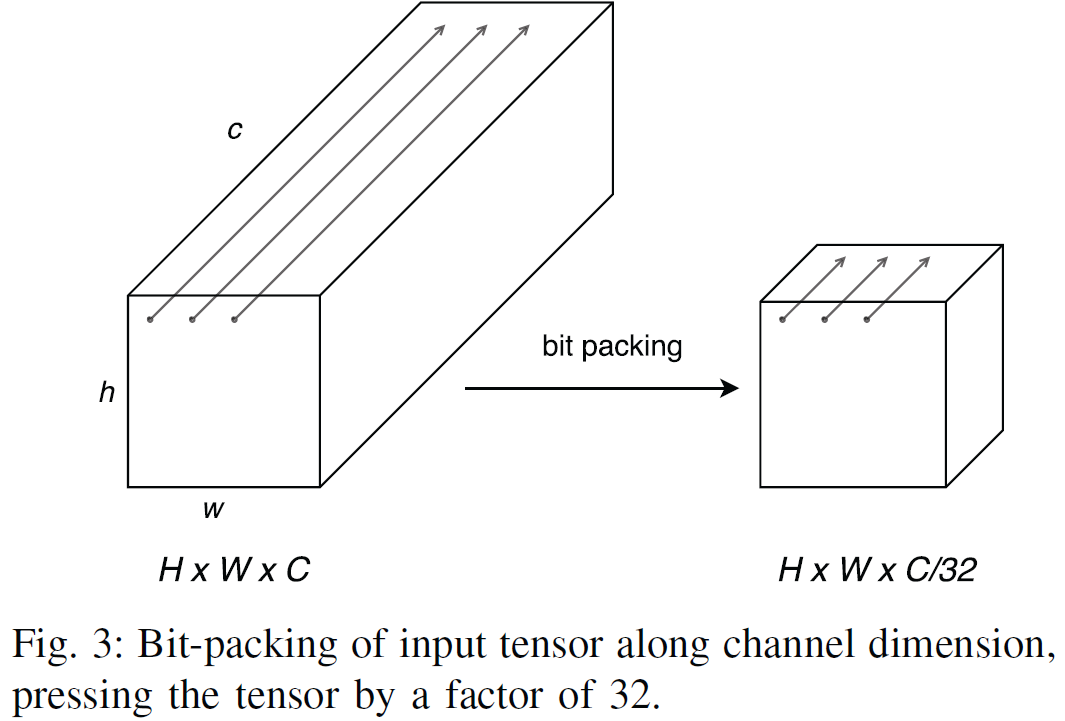
Pressed-Conv Algorithm

Pressed-Conv conducts bit-packing of input tensor and filters along the channel dimension, thus pressing them by a factor of 32 (or 64, 128, 256, 512), and then computes convolution of the pressed input tensor and filters.

Locality-aware Layout

For efficient bit-packing, we adopt $NHWC$ (batch, height, weight, channel) data layout in BitFlow, rather than $NCHW$. According to the layout, the element $A_{h,w,c}$ is found at position $(hW + w)C + c$ in linear memory. Bit packing is performed along the channel dimension, and this enables efficient memory access.

Bit-packing

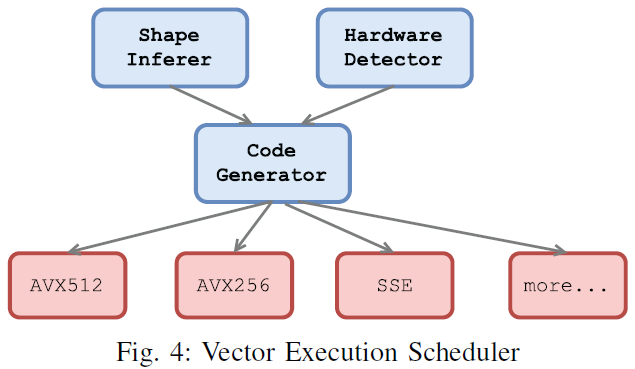
Vector Execution Scheduler

  • When channel dimension is multiple of 512, pack unsigned ints into m512i and utilize AVX512.
  • When channel dimension is multiple of 256, pack unsigned ints into m256i and utilize AVX256.
  • When channel dimension is multiple of 128, pack unsigned ints into m128i and utilize SSE.
  • When channel dimension is multiple of 32, use intrinsic

Vector Execution Scheduler

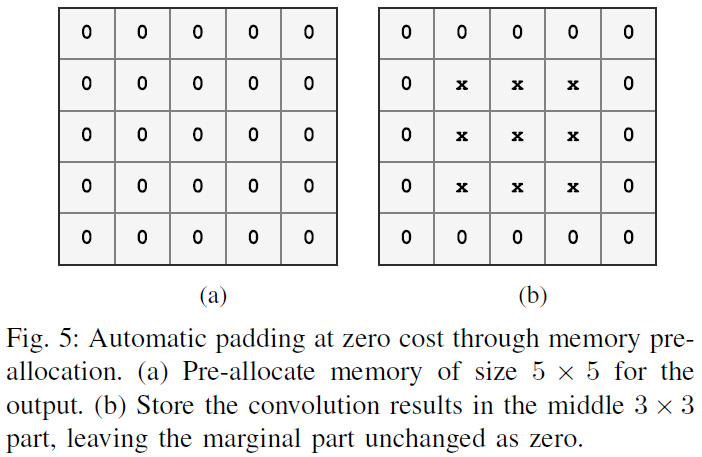
Address Zero Padding

Assume that the output size of a convolution operator is $H×W$ (one channel) without padding, and we want to pad it to $(H+2)×(W+2)$. We pre-allocate memory of size $(H+2)×(W+2)$ for the output, and store the convolution results in the middle $H×W$ part, leaving the marginal part unchanged (zero as initialized).

Address Zero Padding